Bài 1.81 trang 47 SBT hình học 10
Giải bài 1.81 trang 47 sách bài tập hình học 10. Cho hình bình hành ABCD tâm O. Tìm khẳng định sai trong các khẳng định sau:...
Đề bài
Cho hình bình hành \(ABCD\) tâm \(O\). Tìm khẳng định sai trong các khẳng định sau:
A. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
B. \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)
C. \(\overrightarrow {AO} = \overrightarrow {BO} \)
D. \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CB} \)
Phương pháp giải - Xem chi tiết
Dựng hình, nhận xét tính đúng sai của mỗi đáp án và kết luận.
Sử dụng các quy tắc cộng, trừ véc tơ và quy tắc hình bình hành.
Lời giải chi tiết
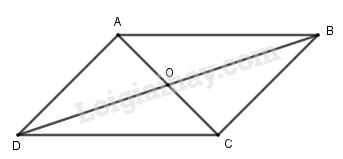
Đáp án A: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) đúng theo quy tắc hình bình hành.
Đáp án B: \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \) đúng theo quy tắc trừ.
Đáp án C: Sai do hai véc tơ \(\overrightarrow {AO} \) và \(\overrightarrow {BO} \) không cùng phương.
Đáp án D: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {CB} \) nên D đúng.
Chọn C.
Loigiaihay.com













Danh sách bình luận