Bài 1.34 trang 32 SBT hình học 10
Giải bài 1.34 trang 32 sách bài tập hình học 10. Cho tam giác ABC...
Cho tam giác \(ABC\).
LG a
Tìm điểm \(K\) sao cho \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} \).
Phương pháp giải:
Xen thêm điểm thích hợp vào các véc tơ và suy ra kết luận.
Giải chi tiết:
\(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow {CB} \)
\( \Leftrightarrow \overrightarrow {KA} + \overrightarrow {KB} + \overrightarrow {KB} = \overrightarrow {CB} \)
\( \Leftrightarrow \left( {\overrightarrow {KA} + \overrightarrow {KB} } \right) + \left( {\overrightarrow {KB} - \overrightarrow {CB} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {KA} + \overrightarrow {KB} + \left( {\overrightarrow {KB} + \overrightarrow {BC} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {KA} + \overrightarrow {KB} + \overrightarrow {KC} = \overrightarrow 0 \)
\( \Leftrightarrow \)\(K\) là trọng tâm của tam giác \(ABC\).
LG b
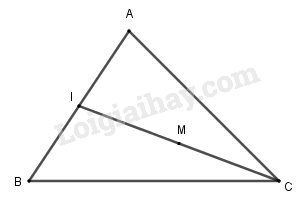
Tìm điểm \(M\) sao cho \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \).
Phương pháp giải:
Xen thêm điểm thích hợp vào các véc tơ và suy ra kết luận.
Giải chi tiết:
\(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow M C = \overrightarrow 0 \) (\(I\) là trung điểm của \(AB\))
Hay \(\overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \)\(\Leftrightarrow M\) là trung điểm của \(IC\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.35 trang 32 SBT hình học 10
- Bài 1.33 trang 32 SBT hình học 10
- Bài 1.32 trang 32 SBT hình học 10
- Bài 1.31 trang 32 SBT hình học 10
- Bài 1.30 trang 32 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS 2K10 Tham Gia Nhóm Zalo Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
Danh sách bình luận