-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 1.28 trang 32 SBT hình học 10
Giải bài 1.28 trang 32 sách bài tập hình học 10. Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN.
Đề bài
Cho tam giác \(ABC\). Gọi \(M\) là trung điểm của \(AB\) và \(N\) là một điểm trên cạnh \(AC\) sao cho \(NA = 2NC\). Gọi \(K\) là trung điểm của \(MN\). Phân tích vec tơ \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
Phương pháp giải - Xem chi tiết
Sử dụng quy tắc trung điểm và mối quan hệ giữa các véc tơ để biểu diễn.
Lời giải chi tiết
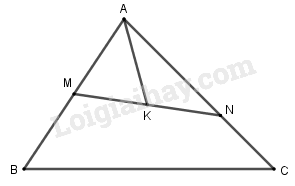
Ta có: \(\overrightarrow {AK} = \dfrac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right)\)\( = \dfrac{1}{2}\left( {\dfrac{1}{2}\overrightarrow {AB} + \dfrac{2}{3}\overrightarrow {AC} } \right)\)\( = \dfrac{1}{4}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.29 trang 32 SBT hình học 10
- Bài 1.30 trang 32 SBT hình học 10
- Bài 1.31 trang 32 SBT hình học 10
- Bài 1.32 trang 32 SBT hình học 10
- Bài 1.33 trang 32 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
