Bài tập 2 trang 122 Tài liệu dạy – học Toán 8 tập 2

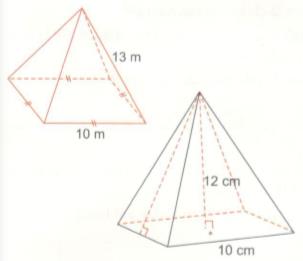
Giải bài tập Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây:

Đề bài

Tính diện tích xung quanh của các hình chóp tứ giác đều sau đây:

Lời giải chi tiết

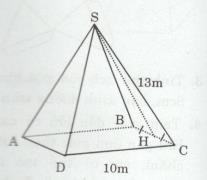
• Gọi H là trung điểm của BC

\(HC = {{BC} \over 2} = {{10} \over 2} = 5(cm)\)

∆SBC cân tại S có SH là đường trung tuyến

(H là trung điểm của BC)

=> SH cũng là đường cao \( \Rightarrow SH \bot BC\) tại H

∆SHC vuông tại H có \(S{H^2} + H{C^2} = S{C^2}\) (định lí Py-ta-go)

\( \Rightarrow S{H^2} + {5^2} = {13^2}\)

\(\Rightarrow S{H^2} = 144\)

\(\Rightarrow SH = 12(cm)\)

Diện tích xung quanh của hình chóp là: \({S_{xq}} = pd = (10 + 10).12 = 240(c{m^2})\)

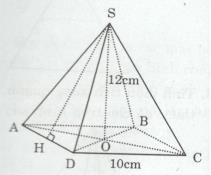
• DC = AB = BC = AD = 10 (cm)

∆SAD cân tại S có SH là đường cao (gt)

=> SH cũng là đường trung tuyến

=> H là trung điểm của AD

Tứ giác ABCD là hình vuông \( \Rightarrow AC \bot BD\) tại O

∆OAD vuông tại O có OH là đường trung tuyến (H là trung điểm của AD)

\( \Rightarrow OH = {{AD} \over 2} = {{10} \over 2} = 5(cm)\)

\(SO \bot (ABCD) \Rightarrow SO \bot HO \Rightarrow \Delta SHO\) vuông tại O

\( \Rightarrow S{H^2} = S{O^2} + H{O^2}\) (định lí Py-ta-go) \( \Rightarrow S{H^2} = {12^2} + {5^2} = 169\)

\(\Rightarrow SH = 13(cm)\)

Diện tích xung quanh của hình chóp là: \({S_{xq}} = p.d = (10 + 10).13 = 260(c{m^2})\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tập 3 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính thể tích của một hình chóp tam giác đều, biết chiều cao của hình chóp là 8 cm, bán kính đường tròn ngoại tiếp tam giác đáy bằng 12 cm.
Bài tập 4 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tam giác đều lớn có cạnh là 8 cm. Khi gấp tam giác theo đường có gạch chấm, em có thể tạo thành hình chóp được không ? Tính diện tích toàn phần hình chóp đó ?
Bài tập 5 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Trong các hình sau, hình nào có thể gấp được thành hình chóp tứ giác đều ?
Bài tập 6 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính diện tích xung quanh, diện tích toàn phần của các hình chóp đều với kích thước đã cho trên hình sau đây:
Bài tập 7 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Bác Lan muốn may một cái lều cắm trại bằng vải bạt cói dạng hình chóp tứ giác đều với kích thước đã cho trên hình. Em hãy cho biết:
Bài tập 1 trang 122 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Hãy cắt hình sau, bôi hồ vào phần mép gấp hình thang, gấp và dán lại để được một hình chóp. Hãy đặt và gọi tên hình chóp đó.