Bài tập 10 trang 123 Tài liệu dạy – học Toán 8 tập 2

Giải bài tập Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên dài 2a. Tính theo a độ dài đường cao của hình chóp.

Đề bài

Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên dài 2a. Tính theo a độ dài đường cao của hình chóp.

Lời giải chi tiết

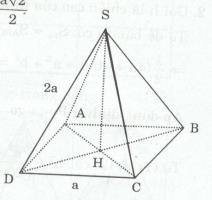
ABCD là tứ giác đều => ABCD là hình vuông \( \Rightarrow AD \bot AB\) tại A

\( \Rightarrow D{B^2} = A{D^2} + A{B^2}\) (định lí Py-ta-go)

\( \Rightarrow D{B^2} = 2{a^2} \Rightarrow DB = a\sqrt 2 ,\) mà \(DH = {{DB} \over 2} \Rightarrow DH = {{a\sqrt 2 } \over 2}\)

∆SDH vuông tại H có: \(S{H^2} + D{H^2} = S{D^2}\) (định lí Py-ta-go)

\(\eqalign{ & \Rightarrow S{H^2} + {{{a^2}} \over 2} = {(2a)^2} \cr&\Rightarrow S{H^2} = 4{a^2} - {{{a^2}} \over 2} = {{7{a^2}} \over 2} \cr & \Rightarrow SH = {{\sqrt {14} } \over 2}a \cr} \)

Vậy độ dài đường cao của hình chóp là \({{\sqrt {14} } \over 2}a\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài tập 11 trang 123 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Hình sau đây được ghép bởi hai hình vuông và bốn hình thang cân bằng nhau với kích thước đã cho. Em hãy:
Bài tập 9 trang 123 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính diện tích toàn phần của:
Bài tập 8 trang 123 Tài liệu dạy – học Toán 8 tập 2
Giải bài tập Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh bên dài 20 cm và cạnh đáy dài 10 cm.