-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Ôn tập chương I - Phép dời hình và phép đồng dạng trong..
Bài 5 trang 35 SGK Hình học 11
Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Đề bài
Cho hình chữ nhật \(ABCD\). Gọi \(O\) là tâm đối xứng của nó. Gọi \(I, F, J, E\) lần lượt là trung điểm của các cạnh \(AB, BC, CD, DA\). Tìm ảnh của tam giác \(AEO\) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng \(IJ\) và phép vị tự tâm \(B\), tỉ số \(2\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
\({Đ_d}\left( M \right) = M' \Leftrightarrow d\) là đường trung trực của MM'.
\({V_{\left( {B;2} \right)}}\left( M \right) = M' \Leftrightarrow \overrightarrow {BM'} = 2\overrightarrow {BM} \).
Lời giải chi tiết
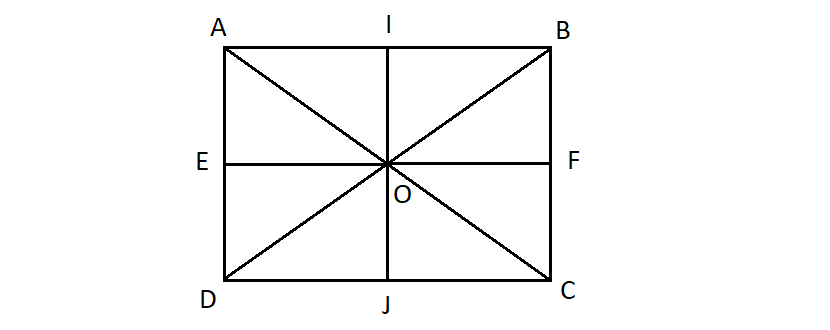
\(IJ\) là đường trung trực của\( AB\) và \(EF\)
Do đó:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{Đ_{IJ}}\left( A \right) = B\\
{Đ_{IJ}}\left( E \right) = F\\
{Đ_{IJ}}\left( O \right) = O
\end{array} \right. \\\Rightarrow {Đ_{IJ}}\left( {\Delta AEO} \right) = \Delta BFO\\
\overrightarrow {BC} = 2\overrightarrow {BF} ,\overrightarrow {BD} = 2\overrightarrow {BO}\\ \Rightarrow \left\{ \begin{array}{l}
{V_{\left( {B;2} \right)}}\left( B \right) = B\\
{V_{\left( {B;2} \right)}}\left( F \right) = C\\
{V_{\left( {B;2} \right)}}\left( O \right) = D
\end{array} \right.\\ \Rightarrow {V_{\left( {B;2} \right)}}\left( {\Delta BFO} \right) = \Delta BCD
\end{array}\)
Vậy ảnh của tam giác \(AEO\) qua phép đồng dạng đã cho là tam giác \(BCD\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 35 SGK Hình học 11
- Bài 7 trang 35 SGK Hình học 11
- Bài 1 trang 35 SGK Hình học 11
- Bài 2 trang 35 SGK Hình học 11
- Bài 3 trang 35 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
