Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Ôn tập chương I - Phép dời hình và phép đồng dạng trong..

Bài 4 trang 34 SGK Hình học 11


Đề bài

Cho vectơ \( \overrightarrow{v}\), đường thẳng \(d\) vuông góc với giá của vectơ \( \overrightarrow{v}\). Gọi \(d'\) là ảnh của \(d\) qua phép tịnh tiến theo vectơ \( \dfrac{1}{2}\) \( \overrightarrow{v}\). Chứng minh rằng phép tịnh tiến theo vectơ \( \overrightarrow{v}\) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng định nghĩa phép tịnh tiến và phép đối xứng trục.

Phép tịnh tiến theo vector \(\overrightarrow v \) biến điểm \(A\) thành điểm \(A’\) \( \Leftrightarrow \overrightarrow {AA'}  = \overrightarrow v \).

Phép đối xứng trục \(d\) biến điểm \(A\) thành \(A’\) \( \Leftrightarrow \) \(d\) là trung trực của \(AA’.\)

Lời giải chi tiết

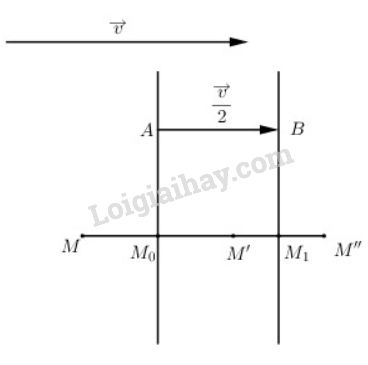
Lấy \(A\) bất kì thuộc đường thẳng \(d,\) xác định điểm \(B\) sao cho \(\overrightarrow {AB}  = {{\overrightarrow v } \over 2}\), qua \(B\) kẻ đường thẳng \(d’ // d\). Khi đó \(d’\) chính là ảnh của đường thẳng \(d\) qua phép tịnh tiến theo vector \({{\overrightarrow v } \over 2}\).

Lấy M\) là một điểm bất kì, gọi \(M' = {D_d}\left( M \right);\,\,M'' = {D_{d'}}\left( {M'} \right)\)

Gọi \({M_0} = MM' \cap d;\,\,{M_1} = M'M'' \cap d' \Rightarrow {M_0}\) và \({M_1}\) lần lượt là trung điểm của \(MM'\) và \(M'M''\).

Ta có \(\overrightarrow {MM'}  = 2\overrightarrow {{M_0}M'} ;\,\,\overrightarrow {M'M''}  = 2\overrightarrow {M'{M_1}} \)

\(\eqalign{  &  \Rightarrow \overrightarrow {MM''}  = \overrightarrow {MM'}  + \overrightarrow {M'M''}  = 2\overrightarrow {{M_0}M'}  + 2\overrightarrow {M'{M_1}}   \cr   & = 2\left( {\overrightarrow {{M_0}M'}  + \overrightarrow {M'{M_1}} } \right) = 2\overrightarrow {{M_0}{M_1}}  = 2\overrightarrow {AB}  \cr&= \overrightarrow v   \cr   &  \Rightarrow {T_{\overrightarrow v }}\left( M \right) = M'' \cr} \)

Vậy phép tịnh tiến theo vector \(\overrightarrow v \) là kết quả của việc thực hiện liên tiếp phép đối xứng qua các đường thẳng \(d\) và \(d'\).

Loigiaihay.com


Bình chọn:
4.5 trên 15 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua