Lớp 12-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
- Bài 1. Phép biến hình
- Bài 2. Phép tịnh tiến
- Bài 3. Phép đối xứng trục
- Bài 4. Phép đối xứng tâm
- Bài 5. Phép quay
- Bài 6. Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7. Phép vị tự
- Bài 8. Phép đồng dạng
- Ôn tập Chương I - Phép dời hình và phép đồng dạng trong mặt phẳng
- Đề kiểm tra 15 phút - Chương 1 - Hình học 11
- Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 11
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
- Đề kiểm tra 15 phút - Chương 2 - Hình học 11
- Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 11
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
- Bài 1. Vectơ trong không gian
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Đường thẳng vuông góc với mặt phẳng
- Bài 4. Hai mặt phẳng vuông góc
- Bài 5. Khoảng cách
- Ôn tập chương III - Vectơ trong không gian. Quan hệ vuông góc trong không gian
- Đề kiểm tra 15 phút - Chương 3 - Hình học 11
- Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 11
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Đề kiểm tra giữa kì 1
-
Đề cương học kì I
-
Đề thi học kì 1 mới nhất có lời giải
-
Đề kiểm tra giữa kì 2
-
Đề cương học kì II
-
Đề thi học kì 2 mới nhất có lời giải
-
Câu hỏi tự luyện Toán 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 1. Đại cương về đường thẳng và mặt phẳng
Bài 4 trang 53 SGK Hình học 11
Đề bài
Cho bốn điểm \(A, B, C\) và \(D\) không đồng phẳng. Gọi \({G_{A}}^{}\), \({G_{B}}^{}\), \({G_{C},{G_{D}}^{}}^{}\) lần lượt là trọng tâm của tam giác \(BCD, CDA, ABD, ABC\). Chứng minh rằng, \(A{G_{A},B{G_{B},C{G_{C},D{G_{D}}^{}}^{}}^{}}^{}\) đồng quy.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sủ dụng kết quả bài tập 3:
Cho ba đường thẳng \({d_{1,}}{d_2},{d_3}\) không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Khi đó ba đường thẳng trên đồng quy.
Lời giải chi tiết
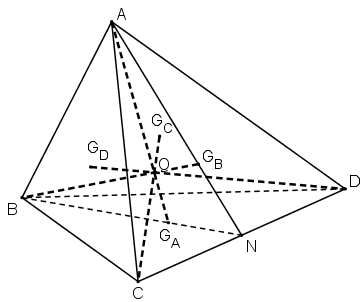
Gọi \(N\) là trung điểm \(CD\).
+ \({G_A}\) là trọng tâm \(\Delta BCD\)
⇒ \({G_A}\) thuộc trung tuyến \(BN\; \subset \;\left( {ANB} \right)\)
⇒ \({AG_A} ⊂ (ANB)\)
\({G_B}\) là trọng tâm \(ΔACD\)
⇒ \({G_B}\) thuộc trung tuyến \(AN ⊂ (ANB)\)
⇒ \({BG_B} ⊂ (ANB).\)
Trong \(\left( {ANB} \right):{\rm{ }}A{G_A}\) không song song với \({BG_B}\)
⇒ \({AG_A}\) cắt \({BG_B}\) tại \(O\)
+ Chứng minh tương tự: \({BG_B}\) cắt \(C{G_C};{\rm{ }}C{G_C}\) cắt \({AG_A}\).
+ \(C{G_C}\) không nằm trong \(\left( {ANB} \right)\; \Rightarrow \;A{G_A};{\rm{ }}B{G_B};{\rm{ }}C{G_C}\;\) không đồng phẳng và đôi một cắt nhau.
Áp dụng kết quả bài 3 \( \Rightarrow {\rm{ }}A{G_A};{\rm{ }}B{G_B};{\rm{ }}C{G_C}\) đồng quy tại \(O\)
+ Chứng minh hoàn toàn tương tự: \(\;A{G_A};{\rm{ }}B{G_B};{\rm{ }}D{G_D}\) đồng quy tại \(O\)
Vậy \(A{G_A};{\rm{ }}B{G_B}\;;{\rm{ }}C{G_C};{\rm{ }}D{G_D}\) đồng quy tại \(O\) (đpcm).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 53 SGK Hình học 11
- Bài 6 trang 54 SGK Hình học 11
- Bài 7 trang 54 SGK Hình học 11
- Bài 8 trang 54 SGK Hình học 11
- Bài 9 trang 54 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
>> Luyện thi TN THPT & ĐH năm 2023 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.
 |
 |
 |
 |
 |
 |
 |
 |
Copyright © 2021 loigiaihay.com
