Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 1. Hàm số lượng giác

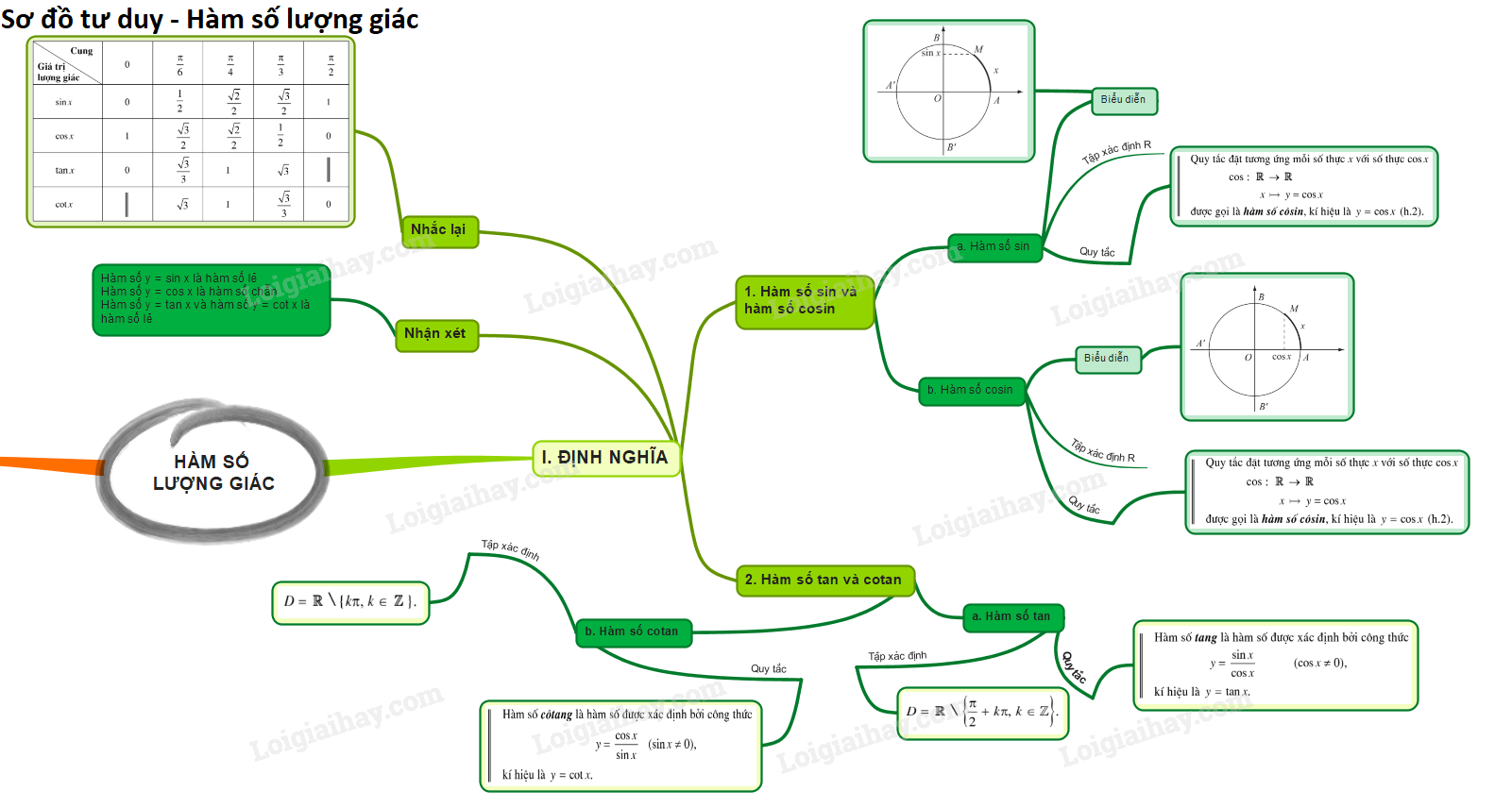
Lý thuyết hàm số lượng giác


1. Hàm số y = sin x và hàm số y = cos x

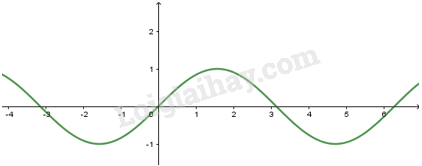
1. Hàm số \(y = \sin x\)

- Có TXĐ \(D = R\), là hàm số lẻ, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\). 

- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k2\pi ;\dfrac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\dfrac{\pi }{2} + k2\pi ;\dfrac{{3\pi }}{2} + k2\pi } \right)\)

- Có đồ thị là đường hình sin đi qua điểm \(O\left( {0;0} \right)\)

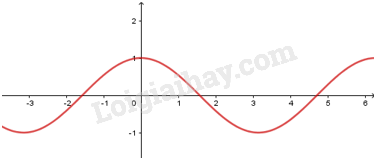
2. Hàm số \(y = \cos x\)

- Có TXĐ \(D = R\), là hàm số chẵn, tuần hoàn với chu kì \(2\pi \), nhận mọi giá trị thuộc đoạn \(\left[ { - 1;1} \right]\).

- Đồng biến trên mỗi khoảng \(\left( { - \pi  + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\)

- Có đồ thị là đường hình sin đi qua điểm \(\left( {0;1} \right)\)

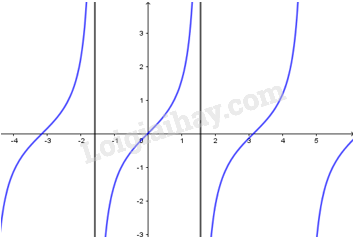
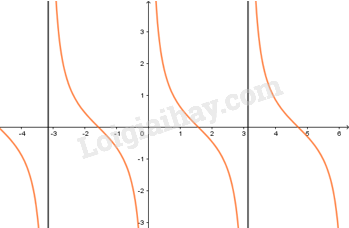
3. Hàm số \(y = \tan x\)

- Có TXĐ \(D = R\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).

- Đồng biến trên mỗi khoảng \(\left( { - \dfrac{\pi }{2} + k\pi ;\dfrac{\pi }{2} + k\pi } \right)\).

4. Hàm số \(y = \cot x\)

- Có TXĐ \(D = R\backslash \left\{ {k\pi ,k \in Z} \right\}\), là hàm số lẻ, tuần hoàn với chu kì \(\pi \), nhận mọi giá trị thuộc \(R\).

- Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi  + k\pi } \right)\).

 

 


Loigiaihay.com


Bình chọn:
4.4 trên 79 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store