 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 1. Hàm số lượng giác
Bài 1. Hàm số lượng giác
Giải bài 1 trang 17 SGK Đại số và Giải tích 11
Hãy xác định các giá trị của x trên đoạn
Video hướng dẫn giải
Hãy xác định các giá trị của \(x\) trên đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\) để hàm số \(y = \tan x\);
LG a
Nhận giá trị bằng \(0\);
Phương pháp giải:
B1: Vẽ đường thẳng y=0 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=0 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
Lời giải chi tiết:
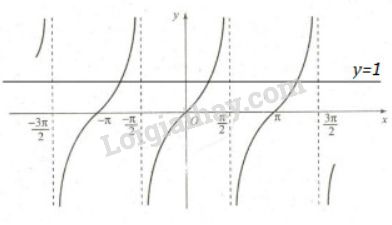
Trong đoạn \(\displaystyle\left[ { - \pi ;{{3\pi } \over 2}} \right]\),
Trục hoành cắt đồ thị hàm số \(y = \tan x\) tại ba điểm có hoành độ \(- π ; 0 ; π\).
Vậy \(x = - π; x = 0 ; x = π\).
LG b
Nhận giá trị bằng \(1\);
Phương pháp giải:
B1: Vẽ đường thẳng y=1 (Ox)
B2: Quan sát xem đồ thị hàm số cắt đường thẳng y=1 tại những điểm nào.
B3: Chỉ lấy những điểm thuộc đoạn đã cho và KL.
Lời giải chi tiết:
Đường thẳng \(y = 1\) cắt đồ thị \(y = \tan x\) tại ba điểm có hoành độ \(\displaystyle {\pi \over 4};{\pi \over 4} \pm \pi \).
Vậy \(\displaystyle x = - {{3\pi } \over 4};\,\,x = {\pi \over 4};\,\,x = {{5\pi } \over 4}\).
LG c
Nhận giá trị dương;
Phương pháp giải:
B1: Quan sát đồ thị hàm số, tìm các giá trị x sao cho đồ thị nằm phía trên trục hoành (hay tanx >0).
B2. Lấy các điểm thuộc đoạn đề bài yêu cầu và Kết luận.
Lời giải chi tiết:
Trong các khoảng \(\displaystyle\left( { - \pi ; - {\pi \over 2}} \right)\); \(\displaystyle\left( {0;{\pi \over 2}} \right)\); \(\displaystyle \left( {\pi ;{{3\pi } \over 2}} \right)\), đồ thị hàm số nằm phía trên trục hoành.
Vậy \(\displaystyle x \in \left( { - \pi ; - {\pi \over 2}} \right) \cup \left( {0;{\pi \over 2}} \right) \cup \left( {\pi ;{{3\pi } \over 2}} \right)\)
LG d
Nhận giá trị âm.
Phương pháp giải:
Quan sát đồ thị hàm số, tìm các điểm thỏa mãn yêu cầu bài toán.
Lời giải chi tiết:
Trong các khoảng \(\displaystyle\left( { - {\pi \over 2};0} \right),\left( {{\pi \over 2};\pi } \right)\), đồ thị hàm số nằm phía dưới trục hoành.
Vậy \(\displaystyle x \in \left( { - {\pi \over 2};0} \right) \cup \left( {{\pi \over 2};\pi } \right)\).
Loigiaihay.com












Danh sách bình luận