Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 1. Hàm số lượng giác

Giải bài 4 trang 17 SGK Đại số và Giải tích 11


Chứng minh rằng

Đề bài

Chứng minh rằng \(sin2(x + kπ) = sin 2x\) với mọi số nguyên \(k\). Từ đó vẽ đồ thị hàm số \(y = sin2x\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tính tuần hoàn và chu kì của hàm số \(y = \sin x\): Hàm \(y = \sin x\) là hàm tuần hoàn với chu kì \(2\pi\).

Lời giải chi tiết

Hàm \(y = \sin x\) là hàm tuần hoàn với chu kì \(2\pi\) nên ta có: 

\(\sin 2\left( {x + k\pi } \right) = \sin \left( {2x + k2\pi } \right) \)\(= \sin 2x\,\,\forall k \in Z\)

Ta có:

\(\begin{array}{l}f\left( x \right) = \sin 2x\\\Rightarrow f\left( {x + \pi } \right) = \sin 2\left( {x + \pi } \right) \\ = \sin \left( {2x + k2\pi } \right) = \sin 2x = f\left( x \right)\end{array}\)

\( \Rightarrow \) Hàm số \(y=sin2x\) tuần là hàm tuần hoàn với chu kì \(\pi\).

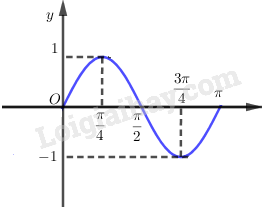
Xét hàm số \(y = \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\).

Ta lấy các điểm đặc biệt như sau:

Từ đó ta có đồ thị hàm số \(y = \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\) là:

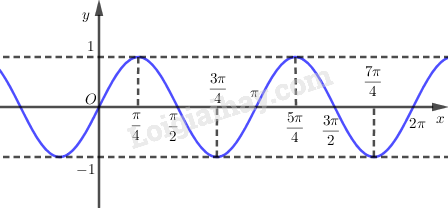
Do hàm số \(y = \sin 2x\) tuần hoàn với chu kì \(\pi \) nên ta có đồ thị là:

 Loigiaihay.com


Bình chọn:
4.3 trên 90 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua