Hoạt động 8 trang 164 Tài liệu dạy – học Toán 8 tập 1

Giải bài tập Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và có độ dài lần lượt là AC = d1, BD = d2 (h.14). Hãy chứng tỏ hình chữ nhật EFGH có diện tích gấp đôi tứ giác ABCD. Từ đó, diện tích tứ giác ABCD.

Đề bài

Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau và có độ dài lần lượt là AC = d₁, BD = d₂ (h.14). Hãy chứng tỏ hình chữ nhật EFGH có diện tích gấp đôi tứ giác ABCD. Từ đó, diện tích tứ giác ABCD.

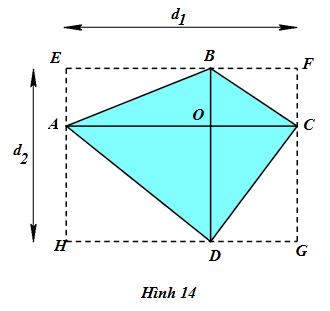
Lời giải chi tiết

\({S_{EBOA}} = OA.OB\) (EBOA là hình chữ nhật),

\({S_{OAB}} = {1 \over 2}OA.OB\) (\(\Delta OAB\) vuông tại O)

Do đó \({S_{EBOA}} = 2{S_{OAB}}\)

Tương tự: \({S_{BFCO}} = 2{S_{OBC}},\,\,{S_{OCGD}} = 2{S_{OCD}},\,\,{S_{AODH}} = {S_{OAD}}\)

Do vậy

\(\eqalign{ & {S_{EFGH}} = {S_{EBOA}} + {S_{BFCO}} + {S_{OCGD}} + {S_{AODH}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 2{S_{OAB}} + 2{S_{OBC}} + 2{S_{OCD}} + 2{S_{OAD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 2\left( {{S_{OAB}} + {S_{OBC}} + {S_{OCD}} + {S_{OAD}}} \right) = 2{S_{ABCD}} \cr} \)

Mà \({S_{EFGH}} = {d_1}{d_2}\)

Do đó \(2{S_{ABCD}} = {d_1}{d_2}\).

Vậy \({S_{ABCD}} = {1 \over 2}{d_1}{d_2}\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Thử tài bạn trang 165 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Tùng làm một cacis diều có thân là hình tứ giác ABCD. Cho biết AC là trung trực của BD và AC = 90 cm, BD = 60 cm (h.16). Em hãy tính diện tích thân diều.
Bạn nào đúng trang 165 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Mai nói ta vẫn có thể tính diện tích hình thoi theo công thức S = d.h.

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý