-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Giải SBT toán hình học và đại số 10 cơ bản
Ôn tập chương 6: Cung và góc lượng giác, công thức lượn..
Bài 6.53 trang 192 SBT đại số 10
Giải bài 6.53 trang 192 sách bài tập đại số 10. Chứng minh các đẳng thức...
Chứng minh rằng các biểu thức sau là những số không phụ thuộc α
LG a
a) A = 2(sin6α + cos6α) - 3(sin4α + cos4α)
Lời giải chi tiết:
A = 2(sin2α + cos2α)(sin4α + cos4α - sin2αcos2α) - 3(sin4α + cos4α)
= -sin4α - cos4α - 2sin2αcos2α
= -(sin2α + cos2α)2 = -1
Cách khác:
A = 2(sin6α + cos6α) - 3(sin4α + cos4α)
=2[ (sin2α + cos2α)3-3 sin2α.cos2α(sin2α + cos2α)] -3[(sin2α + cos2α)2-2sin2α.cos2α]
=2[1-3 sin2α.cos2α]-3[1-2sin2α.cos2α]
=2-6 sin2α.cos2α-3+6 sin2α.cos2α
=-1
LG b
b) B = 4(sin4α + sin4α) - cos4α
Lời giải chi tiết:
b) A = 4[(sin2α + cos2α)2 - 2sin2αcos2α] - cos4α
=4[1-2sin2αcos2α] - cos4α
=4-8 sin2αcos2α- cos4α
=4-2.(2sinα.cosα)2 – (1 - 2sin22α)
=4 – 2 sin22α - 1 + 2sin22α = 3
LG c
c) C = 8(cos8α - sin8α) - cos6α - 7cos2α
Lời giải chi tiết:
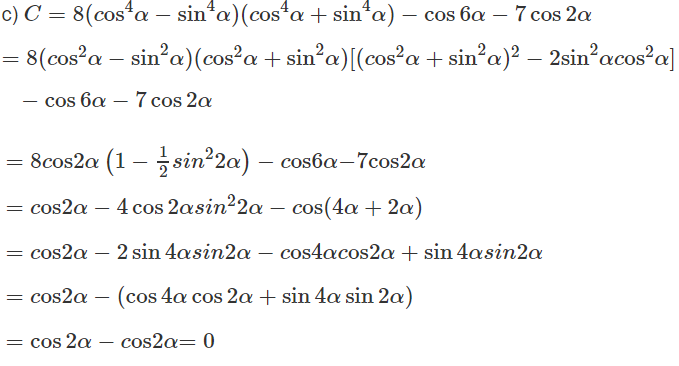
Loigiaihay.com
Bình luận
Chia sẻ
- Bài tập trắc nghiệm trang 193 SBT Đại số 10
- Bài 6.54 trang 193 SBT đại số 10
- Bài 6.55 trang 193 SBT đại số 10
- Bài 6.56 trang 193 SBT đại số 10
- Bài 6.52 trang 192 SBT đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
