Giải bài tập Trên một mảnh vườn hình vuông với độ dài cạnh là 2x (dm), người ta trồng xung quanh một luống hoa có bề rộng 4 dm
Đề bài
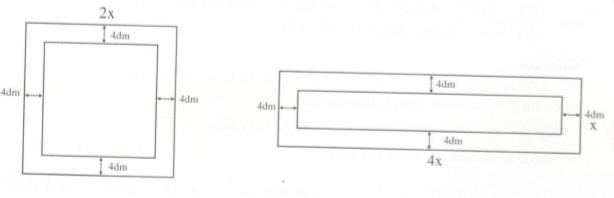
Trên một mảnh vườn hình vuông với độ dài cạnh là 2x (dm), người ta trồng xung quanh một luống hoa có bề rộng 4 dm với diện tích là S1 (dm2). Trên một mảnh vườn hình chữ nhật có độ dài cạnh là x (dm) và 4x (dm), người ta trồng một luống hoa có bề rộng 4 dm với diện tích là S2 (dm2). Em hãy tính S1 và S2 rồi lập tỷ số \({{{S_1}} \over {{S_2}}}\) . Đố em diện tích nào lớn hơn ?
Lời giải chi tiết
Phần đất không trồng hoa của mảnh đất hình vuông là hình vuông cạnh là:
\(2x - 4.2 = 2x - 8\,\,\left( {dm} \right)\)
Diện tích phần đất đó là: \(\left( {2x - 8} \right)\left( {2x - 8} \right) = {\left( {2x - 8} \right)^2}\,\,\left( {d{m^2}} \right)\)
Diện tích mảnh vườn hình vuông là \(\left( {2x} \right)\left( {2x} \right) = 4{x^2}\,\,\left( {d{m^2}} \right)\)
Ta có: \({S_1} = 4{x^2} - {\left( {2x - 8} \right)^2} = 4{x^2} - 4{x^2} + 32x - 64 = 32x - 64\)
Phần đất không trồng hoa của mảnh vườn hình chữ nhật là hình chữ nhật có độ dài cạnh là \(x - 4.2 = x - 8\,\,\left( {dm} \right)\) và \(4x - 4.2 = 4x - 8\,\,\left( {dm} \right)\)
Diện tích phần đất đó là: \(\left( {x - 8} \right)\left( {4x - 8} \right)\,\,\left( {d{m^2}} \right)\)
Diện tích mảnh vườn hình chữ nhật là \(x.4x = 4{x^2}\,\,\left( {d{m^2}} \right)\)
Ta có: \({S_2} = 4{x^2} - \left( {x - 8} \right)\left( {4x - 8} \right) = 4{x^2} - 4{x^2} + 8x + 32x - 64 = 40x - 64\)
Do đó: \({{{S_1}} \over {{S_2}}} = {{32x - 64} \over {40x - 64}}\)
Vì \(40x - 64 > 32x - 64\) nên \({{{S_1}} \over {{S_2}}} < 1\).
Vậy \({S_2} > {S_1}\).
Loigiaihay.com
>>Học trực tuyến lớp 8 trên Tuyensinh247.com mọi lúc, mọi nơi đầy đủ các môn: Toán, Văn, Anh, Lý, Hóa, Sinh, Sử, Địa cùng các thầy cô giáo dạy giỏi, nổi tiếng.
Lớp 12
