Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 4. Cấp số nhân

Bài 6 trang 104 SGK Đại số và Giải tích 11


Cho hình vuông C1 có cạnh bằng 4.

Đề bài

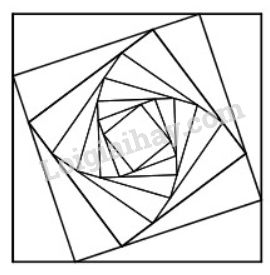
Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (hình bên). Từ hình vuông C2 lại tiếp tục như trên để được hình vuông C3… Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C1, C2, C3, …,Cn

Gọi an là độ dài cạnh của hình vuông Cn. Chứng minh dãy số (an) là một cấp số nhân.

Video hướng dẫn giải

Lời giải chi tiết

Xét dãy số \((a_n)\), ta có \(a_1= 4\).

Gọi \({a_n}\) là cạnh hình vuông \({C_n}\).

Ta tính cạnh hình vuông \({a_{n + 1}}\) như sau:

Xét tam giác \(BEF\) vuông tại \(B\) có \(BE = \dfrac{3}{4}BA = \dfrac{{3{a_n}}}{4}\), \(BF = \dfrac{1}{4}BC = \dfrac{{{a_n}}}{4}\)

Do đó \(EF = \sqrt {B{E^2} + B{F^2}} \) \( = \sqrt {{{\left( {\dfrac{{3{a_n}}}{4}} \right)}^2} + {{\left( {\dfrac{{{a_n}}}{4}} \right)}^2}}  = \dfrac{{\sqrt {10} }}{4}{a_n}\) hay \({a_{n + 1}} = \dfrac{{\sqrt {10} }}{4}{a_n}\).

Vậy dãy số \((a_n)\) là cấp số nhân với số hạng đầu là \(a_1= 4\) và công bội \(\displaystyle q = {{\sqrt {10} } \over 4}\)

 Loigiaihay.com


Bình chọn:
4.4 trên 18 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho Lớp 11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store