 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 2. Phương trình lượng giác cơ bản
Bài 2. Phương trình lượng giác cơ bản
Giải bài 4 trang 29 SGK Đại số và Giải tích 11
Giải phương trình
Đề bài
Giải phương trình \(\displaystyle {{2\cos 2x} \over {1 - \sin 2x}} = 0\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tìm ĐKXĐ.
+) \(\dfrac{A}{B} = 0 \Rightarrow A = 0\)
+) Giải phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\)
Lời giải chi tiết
Điều kiện: \(\sin 2x\neq 1\Leftrightarrow 2x\neq \dfrac{\pi }{2}+k2 \pi \) \(\Leftrightarrow x\neq \dfrac{\pi }{4}+k \pi(k\in \mathbb{Z})\)
\(\displaystyle {{2\cos 2x} \over {1 - \sin 2x}} = 0\)
\(\Rightarrow 2\cos 2x=0\)
\( \Leftrightarrow \cos 2x = 0\)
\(\Leftrightarrow 2x = \dfrac{\pi }{2} + k\pi \)
\(\Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)\)
Kiểm tra ĐK:
\(\dfrac{\pi }{4} + \dfrac{{k\pi }}{2} \ne \dfrac{\pi }{4} + l\pi \)
\( \Leftrightarrow \dfrac{{k\pi }}{2} \ne l\pi \)
\( \Leftrightarrow \dfrac{k}{2} \ne l\)
\(\Leftrightarrow k \ne 2l\)
Hay \(k\) không thể nhận các giá trị chẵn.
Do đó k lẻ nên \(k = 2m + 1\).
Vậy \(x = \dfrac{\pi }{4} + \dfrac{{\left( {2m + 1} \right)\pi }}{2} = \dfrac{{3\pi }}{4} + m\pi \).
Vậy phương trình có nghiệm \(x = \dfrac{{3\pi }}{4} + m\pi ,m\in Z \).
Chú ý: Nghiệm \(x = \dfrac{{3\pi }}{4} + m\pi \) cũng có thể viết thành \(x = - \dfrac{\pi }{4} + n\pi \) bằng cách đặt \(m = n - 1\).
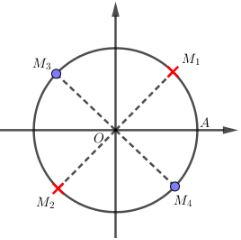
Các em cũng có thể vẽ đường tròn đơn vị để loại nghiệm như sau:
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + k\pi \) là \({M_1},{M_2}\) nhưng điều kiện là \(x \ne \dfrac{\pi }{4} + k\pi \) nên hai điểm này không lấy.
Các điểm biểu diễn \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\) là \({M_1},{M_2},{M_3},{M_4}\) nhưng do không lấy hai điểm \({M_1},{M_2}\) nên các điểm biểu diễn nghiệm chỉ còn \({M_3},{M_4}\).
Dễ thấy hai điểm này đối xứng nhau qua \(O\) và \(\widehat {AO{M_4}} = - \dfrac{\pi }{4}\) nên nghiệm của phương trình là \(x = - \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\).
Loigiaihay.com












Danh sách bình luận