-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: SỐ HỮU TỈ. SỐ THỰC
- Bài 1. Tập hợp Q các số hữu tỉ
- Bài 2. Cộng, trừ số hữu tỉ
- Bài 3. Nhân, chia số hữu tỉ
- Bài 4. Giá trị tuyệt đối của một số hữu tỉ. Cộng, trừ, nhân, chia số thập phân
- Bài 5. Luỹ thừa của một số hữu tỉ
- Bài 6. Luỹ thừa của một số hữu tỉ (tiếp)
- Bài 7. Tỉ lệ thức
- Bài 8. Tính chất của dãy tỉ số bằng nhau
- Bài 9. Số thập phân hữu hạn. Số thập phân vô hạn tuần hoàn
- Bài 10. Làm tròn số
- Bài 11. Số vô tỉ. Khái niệm về căn bậc hai
- Bài 12. Số thực
- Ôn tập chương 1 - Số hữu tỉ. Số thực
-
CHƯƠNG 2: HÀM SỐ VÀ ĐỒ THỊ
- Bài 1. Đại lượng tỉ lệ thuận
- Bài 2. Một số bài toán về đại lượng tỉ lệ thuận
- Bài 3. Đại lượng tỉ lệ nghịch
- Bài 4. Một số bài toán về đại lượng tỉ lệ nghịch
- Bài 5. Hàm số
- Bài 6. Mặt phẳng toạ độ
- Bài 7. Đồ thị của hàm số y = ax (a khác 0)
- Ôn tập chương 2 - Hàm số và đồ thị
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 1
-
CHƯƠNG 1: ĐƯỜNG THẲNG VUÔNG GÓC. ĐƯỜNG THẲNG SONG SONG
- Bài 1. Hai góc đối đỉnh
- Bài 2. Hai đường thẳng vuông góc
- Bài 3. Các góc tạo bởi một đường thẳng cắt hai đường thẳng
- Bài 4. Hai đường thẳng song song
- Bài 5. Tiên đề Ơ-clit về đường thẳng song song
- Bài 6. Từ vuông góc đến song song
- Bài 7. Định lí
- Ôn tập chương 1 - Đường thẳng vuông góc. Đường thẳng song song
-
CHƯƠNG 2: TAM GIÁC
- Bài 1. Tổng ba góc của một tam giác
- Bài 2. Hai tam giác bằng nhau
- Bài 3. Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh (c.c.c)
- Bài 4. Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
- Bài 5. Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)
- Bài 6. Tam giác cân
- Bài 7. Định lí Py-ta-go
- Bài 8. Các trường hợp bằng nhau của tam giác vuông
- Bai 9: Thực hành ngoài trời
- Ôn tập chương 2 - Tam giác
-
-
PHẦN ĐẠI SỐ - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: THỐNG KÊ
-
CHƯƠNG 4: BIỂU THỨC ĐẠI SỐ
- Bài 1. Khái niệm về biểu thức đại số
- Bài 2. Giá trị của biểu thức đại số
- Bài 3. Đơn thức
- Bài 4. Đơn thức đồng dạng
- Bài 5. Đa thức
- Bài 6. Cộng, trừ đa thức
- Bài 7. Đa thức một biến
- Bài 8. Cộng, trừ đa thức một biến
- Bài 9. Nghiệm của đa thức một biến
- Bài tập ôn chương 4 - Biểu thức đại số
-
-
PHẦN HÌNH HỌC - SBT TOÁN 7 TẬP 2
-
CHƯƠNG 3: QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC. CÁC ĐƯỜNG ĐỒNG QUY CỦA TAM GIÁC
- Bài 1. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
- Bài 3. Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
- Bài 4. Tính chất ba đường trung tuyến của tam giác
- Bài 5. Tính chất tia phân giác của một góc
- Bài 6. Tính chất ba đường phân giác của tam giác
- Bài 7. Tính chất đường trung trực của một đoạn thẳng
- Bài 8. Tính chất ba đường trung trực của tam giác
- Bài 9. Tính chất ba đường cao của tam giác
- Bài tập ôn chương 3 - Quan hệ giữa các yếu tố trong tam giác. Các đường đồng quy trong tam giác
-
ÔN TẬP CUỐI NĂM
-
Bài 4 trang 100 SBT toán 7 tập 1
Giải bài 4 trang 100 sách bài tập toán 7 tập 1. Vẽ đường tròn tâm O bán kính 2cm...
Đề bài
a) Vẽ đường tròn tâm \(O\) bán kính \(2\,cm.\)
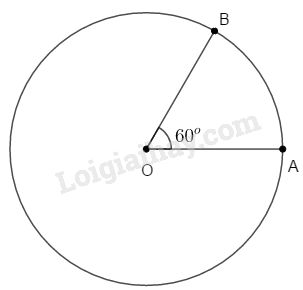
b) Vẽ góc \(AOB\) có số đo bằng \(60^\circ \). Hai điểm \(A, B\) nằm trên đường tròn \((O; 2cm)\).
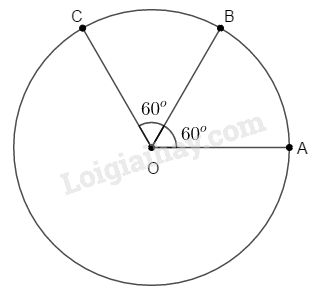
c) Vẽ góc \(BOC\) có số đo bằng \(60^\circ \). Điểm \(C\) thuộc đường tròn \((O; 2cm).\)
d) Vẽ các tia \(OA’, OB’, OC’\) lần lượt là tia đối của các tia \(OA, OB, OC.\) Các điểm \(A’; B’; C’\) thuộc đường tròn \((O; 2cm).\)
e) Viết tên năm cặp góc đối đỉnh.
g) Viết tên năm cặp góc bằng nhau mà không đối đỉnh.
Phương pháp giải - Xem chi tiết
- Định nghĩa: Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
- Tính chất: Hai góc đối đỉnh thì bằng nhau.
- Tổng hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
a)
b)
c)
d)
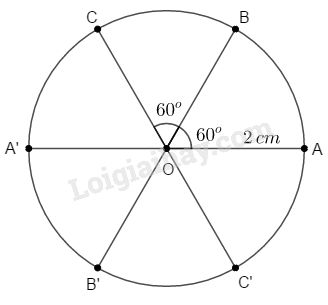
e) Tên \(5\) cặp góc đối đỉnh:
\(\widehat {AOB}\) và \(\widehat {A'OB'}\); \(\widehat {BOC}\) và \(\widehat {B'OC'}\);
\(\widehat {AOC}\) và \(\widehat {A'OC'}\); \(\widehat {AOB'}\) và \(\widehat {BOA'}\);
\(\widehat {AOC'}\) và \(\widehat {A'OC}\)
g) Vì \(\widehat {AOB} + \widehat {BOC} + \widehat {COA'} = 180^\circ \) (kề bù)
\( \Rightarrow \widehat {COA'} = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Tên \(5\) cặp góc bằng nhau không đối đỉnh:
\(\eqalign{
& \widehat {AOB} = \widehat {BOC} = 60^\circ ;\cr&\widehat {BOC} = \widehat {COA'} = 60^\circ \cr
& \widehat {AOB} = \widehat {COA'} = 60^\circ ;\cr
& \widehat {AO{\rm{A}}'} = \widehat {BOB'} = 180^\circ \cr} \)
\(\widehat {A'OB'} = \widehat {B'OC'} = 60^\circ \) (vì \(\widehat {A'OB'} = \widehat {AOB} = 60^\circ \) (hai góc đối đỉnh và \(\widehat {B'OC'} = \widehat {BOC} = 60^\circ \) (hai góc đối đỉnh))
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 100 SBT toán 7 tập 1
- Bài 6 trang 100 SBT toán 7 tập 1
- Bài 7 trang 100 SBT toán 7 tập 1
- Bài 1.1, 1.2, 1.3, 1.4 phần bài tập bổ sung trang 100, 101 SBT toán 7 tập 1
- Bài 3 trang 100 SBT toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
