-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 15 trang 203 SBT Hình học 10
Giải bài 15 trang 203 sách bài tập Hình học 10. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có AB:3x + 5y - 33 = 0 ; đường cao AH:7x + y - 13 = 0; trung tuyến BM:x + 6y - 24 = 0 (M là trung điểm của AC). Tìm phương trình các cạnh còn lại của tam giác.
Đề bài
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có \(AB:3x + 5y - 33 = 0\) ; đường cao \(AH:7x + y - 13 = 0\); trung tuyến \(BM:x + 6y - 24 = 0\) (M là trung điểm của AC). Tìm phương trình các cạnh còn lại của tam giác.
Lời giải chi tiết
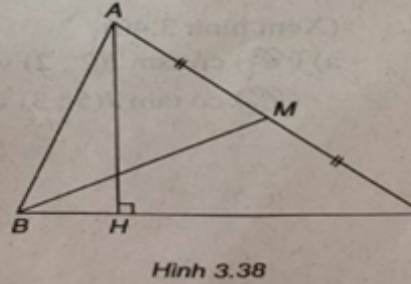
Tọa độ điểm A là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}3x + 5y - 33 = 0\,\,\,\,\,\,\,(AB)\\7x + y - 13 = 0\,\,\,\,\,\,\,\,\,(AH).\end{array} \right.\) Vậy A(1 ; 6)
Tọa độ điểm B là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}3x + 5y - 33 = 0\,\,\,\,\,\,\,(AB)\\x + 6y - 24 = 0\,\,\,\,\,\,\,\,\,(BM)\end{array} \right.\) Vậy B(6 ; 3).
Đặt \(C(x;y)\) ta suy ra trung điểm M của AC có tọa độ \(M\left( {\frac{{x + 1}}{2};\frac{{y + 6}}{2}} \right).\)
Ta có \(\overrightarrow {BC} = \left( {x - 6;y - 3} \right)\)
\({\overrightarrow u _{AH}} = (1; - 7)\)
Ta có \(\left\{ \begin{array}{l}M \in BM\\\overrightarrow {BC} .{\overrightarrow u _{AH}} = 0\end{array} \right.\)
Suy ra tọa độ điểm C là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}\left( {\frac{{x + 1}}{2}} \right) + 6\left( {\frac{{y + 6}}{2}} \right)\\x - 6 - 7(y - 3) = 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}x + 6y - 11 = 0\\x - 7y + 15 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 2.\end{array} \right.\)
Phương trình cạnh \(BC:x - 7y + 15 = 0\)
Phương trình cạnh \(AC:2x - y + 4 = 0.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 16 trang 203 SBT Hình học 10
- Bài 17 trang 203 SBT Hình học 10
- Bài 18 trang 203 SBT Hình học 10
- Bài 19 trang 203 SBT Hình học 10
- Bài 20 trang 203 SBT Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
