-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 14 trang 203 SBT Hình học 10
Giải bài 14 trang 203 sách bài tập Hình học 10. Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật biết tọa độ hai đỉnh đối diện là (1 ; -5) và (6 ; 2), phương trình của một đường chéo là 5x + 7y - 7 = 0. Tìm tọa độ các đỉnh còn lại của hình chữ nhật.
Đề bài
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật biết tọa độ hai đỉnh đối diện là (1 ; -5) và (6 ; 2), phương trình của một đường chéo là \(5x + 7y - 7 = 0\). Tìm tọa độ các đỉnh còn lại của hình chữ nhật.
Lời giải chi tiết
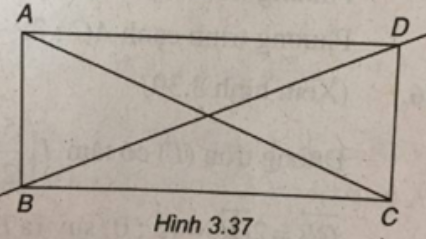
Đặt A(1 ; -5), C(6 ; 2) và BD có phương trình \(5x + 7y - 7 = 0.\)
Đặt \({x_B} = 7t\) ta có \({y_B} = 1 - 5t.\)
Vậy \(B(7t;1 - 5t).\)
Suy ra \(\overrightarrow {BA} = \left( {1 - 7t; - 6 + 5t} \right)\)
\(\overrightarrow {BC} = (6 - 7t;1 + 5t).\)
Ta có \(\overrightarrow {BA} .\overrightarrow {BC} = 0\) \( \Leftrightarrow \left( {1 - 7t} \right)\left( {6 - 7t} \right) + \left( {1 + 5t} \right)\left( { - 6 + 5t} \right) = 0\)
\( \Leftrightarrow 74{t^2} - 74t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 1\end{array} \right.\)
Vậy B(0 ; 1); D(7 ; -4) hoặc B(7 ; -4); D(0 ; 1).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 15 trang 203 SBT Hình học 10
- Bài 16 trang 203 SBT Hình học 10
- Bài 17 trang 203 SBT Hình học 10
- Bài 18 trang 203 SBT Hình học 10
- Bài 19 trang 203 SBT Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
