Giải SBT toán hình học và đại số 11 nâng cao Bài 3: Một số dạng phương trình lượng giác đơn giản

Bài 1.29 trang 12 SBT Đại số và Giải tích 11 Nâng cao


Giải bài 1.29 trang 12 sách bài tập Đại số và Giải tích 11 Nâng cao. Một cách trình bày việc đưa biểu thức ...

Lựa chọn câu để xem lời giải nhanh hơn

Một cách trình bày việc đưa biểu thức \(a\sin x + b\cos x\) (a, b là hằng số, \({a^2} + {b^2} \ne 0\)) về dạng \(C\sin \left( {x + \alpha } \right)\) nhờ biểu thức toạ độ của tích vô hướng của hai vectơ

Trong mặt phẳng tọa độ gắn với đường tròn lượng giác tâm O gốc A, hãy xét các điểm \(P\left( {a;b} \right),Q\left( {b;a} \right),M\left( {\cos x;\sin x} \right)\)

LG a

Từ công thức \(\overrightarrow {OQ} .\overrightarrow {OM}  = a\sin x + b\cos x\) và

\(\overrightarrow {OQ} .\overrightarrow {OM}  = \left| {\overrightarrow {OQ} } \right|.\left| {\overrightarrow {OM} } \right|\cos \left( {OQ,QM} \right)\)

Hãy suy ra \(a\sin x + b\cos x = C\cos \left( {x - \beta  } \right)\) trong đó \(\beta \) là số đo của góc lượng giác \(\left( {OA,OQ} \right)\)

Lời giải chi tiết:

Ta có \(\overrightarrow {OQ} .\overrightarrow {OM}  = a\sin x + b\cos x\)

\(\eqalign{
& = \left| {\overrightarrow {OQ} } \right|.\left| {\overrightarrow {OM} } \right|\cos \left( {OQ,OM} \right) \cr&= \left| {\overrightarrow {OQ} } \right|\cos (\left( {OA,OM} \right) - \left( {OA,OQ} \right)) \cr 
& = \left| {\overrightarrow {OQ} } \right|\cos \left( {\alpha - \beta } \right),\cr&\left| {\overrightarrow {OQ} } \right| = \sqrt {{a^2} + {b^2}} ,\beta = \left( {OA,OQ} \right) \cr} \)

LG b

 Từ câu a) suy ra rằng  \(a\sin x + b\cos x = C\sin \left( {x + \alpha } \right)\) trong đó \(\alpha \) là số đo của góc lượng giác \(\left( {OA,OP} \right),C = \left| {\overrightarrow {OP} } \right|\)

Lời giải chi tiết:

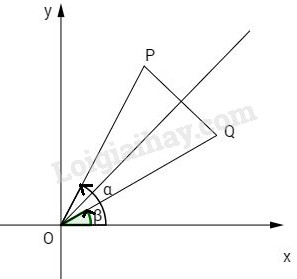
Hai điểm \(P\left( {a;b} \right)\) và \(Q\left( {b;a} \right)\) đối xứng qua đường phân giác của góc phần tư thứ nhất của hệ tọa độ, nên dễ thấy

\(\left( {OA,OQ} \right) = {\pi  \over 2} - \left( {OA,OP} \right),\) tức là

\(\beta  = {\pi  \over 2} - \alpha  + k2\pi ,k \in Z.\)

 Vậy

\(a\sin x + b\cos x = \left| {\overrightarrow {OQ} } \right|\cos \left( {x - \beta } \right)\)

\(= \left| {\overrightarrow {OP} } \right|\cos \left( {x - {\pi  \over 2} + \alpha } \right) \)

\(= \left| {\overrightarrow {OP} } \right|\sin \left( {x + \alpha } \right)\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store