Lý thuyết về giới hạn của hàm số

1. Giới hạn hữu hạn

+) Cho khoảng \(K\) chứa điểm \(x_0\) và hàm số \(y = f(x)\) xác định trên \(K\) hoặc trên \(K\backslash {\{x_0}\rm{\} }.\)

\(\underset{x\rightarrow x_{_{0}}}{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n ∈ K\backslash {\rm{\{ }}{x_0}{\rm{\} }}\) và \(x_n\rightarrow x_0\)_, ta có
\(\lim f(x_n) =L\). 

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((x_0; b)\).

\(\underset{x\rightarrow x_{_{0}}^{+}}{\lim} f(x) = L\) khi và chỉ khi dãy số \((x_n) bất kì, \(x_0<x_n< b\) và \(x_n\rightarrow x_0\) ,ta có \(\lim f(x_n) = L\).

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; x_0)\).

\(\underset{x\rightarrow x_{_{0}}^{-}}{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(a <x_n< x_0\) và \(x_n\rightarrow x_0\), ta có
\(\lim f(x_n) = L\).

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; +∞)\).

\(\underset{x\rightarrow+\infty }{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n> a\), \(x_n\rightarrow +\infty\) thì \(lim f(x_n) = L\).

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((-∞; a)\).

\(\underset{x\rightarrow-\infty }{\lim} f(x) = L\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n< a\), \(x_n\rightarrow -\infty\) thì \(\lim f(x_n) = L\).

2. Giới hạn vô cực

Sau đây là hai trong số nhiều loại giới hạn vô cực khác nhau:

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a; +∞)\), \(\underset{x\rightarrow+\infty }{\lim} f(x) = -∞\) khi và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n> a\), \(x_n\rightarrow +\infty\) thì ta có \(\lim f(x_n) = -∞\)

+) Cho khoảng \(K\) chứa điểm \(x_0\) và hàm số \(y = f(x)\) xác định trên \(K\) hoặc trên \(K\backslash {\{x_0}\rm{\} }.\)

\(\underset{x\rightarrow x_{_{0}}}{\lim} f(x) = +∞\) và chỉ khi với dãy số \((x_n)\) bất kì, \(x_n ∈K\backslash {\rm{\{ }}{x_0}{\rm{\} }}\) và \(x_n\rightarrow x_0\) thì ta có: \(\lim f(x_n) = +∞\).

Nhận xét: \(f(x)\) có giới hạn \(+∞ \) khi và chỉ khi \(-f(x)\) có giới hạn \(-∞\).

3. Các giới hạn đặc biệt

a) \(\underset{x\rightarrow x_{_{0}}}{\lim} x = x_0\);

b) \(\underset{x\rightarrow x_{_{0}}}{\lim}c = c\);

c) \(\underset{x\rightarrow \pm \infty }{\lim} c = c\);

d) \(\underset{x\rightarrow \pm \infty }{\lim}\) \(\frac{c}{x} = 0\) (\(c\) là hằng số);

e) \(\underset{x\rightarrow+\infty }{\lim} x^k= +∞\), với \(k\) nguyên dương;

f) \(\underset{x\rightarrow-\infty }{lim} x^k= -∞\), nếu \(k\) là số lẻ;

g)  \(\underset{x\rightarrow-\infty }{lim}x^k = +∞\) , nếu \(k\) là số chẵn.

4. Định lí về giới hạn hữu hạn

Định lí 1. 

a) Nếu \(\underset{x\rightarrow x_{_{0}}}{lim} = L\) và \(\underset{x\rightarrow x_{_{0}}}{lim}\) \(g(x) = M\) thì:

\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) + g(x)] = L + M\);

\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) - g(x) = L - M\);

\(\underset{x\rightarrow x_{_{0}}}{lim} [f(x) . g(x)] = L.M\);

\(\underset{x\rightarrow x_{_{0}}}{lim}\) \(\frac{f(x)}{g(x)}\)= \(\frac{L}{M}\) (nếu \(M ≠ 0\)).

b) Nếu \(f(x) ≥ 0\) và \(\underset{x\rightarrow x_{_{0}}}{\lim} f(x) = L\), thì \(L ≥ 0\) và \(\underset{x\rightarrow x_{_{0}}}{\lim}\sqrt {f(x)} = \sqrt L\)

Chú ý: Định lí 1 vẫn đúng khi \(x_n\rightarrow +\infty\) hoặc \(x_n\rightarrow -\infty\).

Định lí 2.

\(\underset{x\rightarrow x_{_{0}}}{lim} f(x) = L\) khi và chỉ khi \(\underset{x\rightarrow x_{_{0}}^{+}}{lim}\) f(x) = \(\underset{x\rightarrow x_{_{0}}^{-}}{\lim} f(x) = L\).

5. Quy tắc về giới hạn vô cực

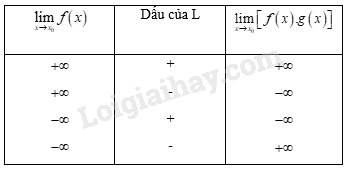
a) Quy tắc giới hạn của tích \(f(x).g(x)\)

+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) =  \pm \infty \) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = L \ne 0\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right).g\left( x \right)} \right]\) được cho trong bảng sau:

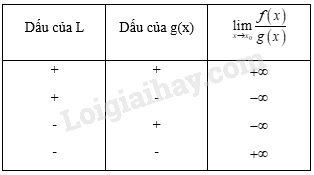
b) Quy tắc tìm giới hạn của thương \(\dfrac{f(x)}{g(x)}\)

+ Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L \ne 0\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\) và \(g\left( x \right) > 0\) hoặc \(g\left( x \right) < 0\) với mọi \(x \in J\backslash \left\{ {{x_0}} \right\}\), trong đó \(J\) là một khoảng nào đó chứa \({x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \dfrac{{f\left( x \right)}}{{g\left( x \right)}}\) được cho trong bảng sau:

Loigiaihay.com