 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Bài 2. Giới hạn của hàm số
Bài 2. Giới hạn của hàm số
Câu hỏi 1 trang 123 SGK Đại số và Giải tích 11
Xét hàm số...
Video hướng dẫn giải
Xét hàm số:
\(\displaystyle f(x) = {{2{x^2} - 2x} \over {x - 1}}\)
LG 1
Cho biến \(x\) những giá trị khác 1 lập thành dãy số \({x_n},{\rm{ }}{x_n}\; \to {\rm{ }}1\) như trong bảng sau:
Khi đó, các giá trị tương ứng của hàm số
\(f({x_1}),{\rm{ }}f({x_2}), \ldots ,{\rm{ }}f({x_n}),{\rm{ }} \ldots \)
cũng lập thành một dãy số mà ta kí hiệu là \((f({x_n})).\)
a) Chứng minh rằng \(f\left( {{x_n}} \right) = 2{x_n} = \dfrac{{2n + 2}}{n}\)
b) Tìm giới hạn của dãy số \((f({x_n})).\)
Phương pháp giải:
a) Tính và rút gọn \(f\left( {{x_n}} \right)\) suy ra đáp số, chú ý \(x_n=\dfrac{{n + 1}}{n}\).
b) Xét giới hạn \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2)\) và suy ra đáp số.
Lời giải chi tiết:
a) \(\displaystyle f({x_n}) = {{2{x_n}^2 - 2{x_n}} \over {{x_n} - 1}} = {{2{x_n}({x_n} - 1)} \over {{x_n} - 1}} \) \(= 2{x_n}\)
\(\displaystyle {x_n} = {{n+1} \over {n}} \) \(\displaystyle \Rightarrow f({x_n}) = 2{x_n} = 2.{{n+1} \over {n}} = {{2n+2} \over {n}}\)
b) \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) \) \(\displaystyle = \mathop {\lim }\limits_{n \to + \infty } ({{2n+2} \over {n}} - 2) = \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}}\)
Ta có: \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}} = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } f({x_n}) = 2\)
LG 2
Chứng minh rằng với dãy số bất kì \({x_n},{\rm{ }}{x_n}\; \ne {\rm{ }}1\) và \({x_n}\; \to {\rm{ }}1\), ta luôn có \(\;f({x_n}) \to 2.\)
(Với tính chất thể hiện trong câu 2, ta nói hàm số \(\displaystyle f(x) = {{2{x^2} - 2x} \over {x - 1}}\) có giới hạn là 2 khi \(x\) dần tới 1).
Phương pháp giải:
Tính \(\lim f({x_n})\) dựa vào công thức có được ở phần 1a.
Lời giải chi tiết:
\(\lim f({x_n}) = \lim\,2{x_n} \) \(= 2\lim {x_n} = 2.1 = 2\)
Loigiaihay.com




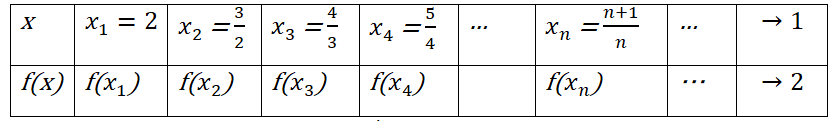








Danh sách bình luận