Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 2. Quy tắc tính đạo hàm

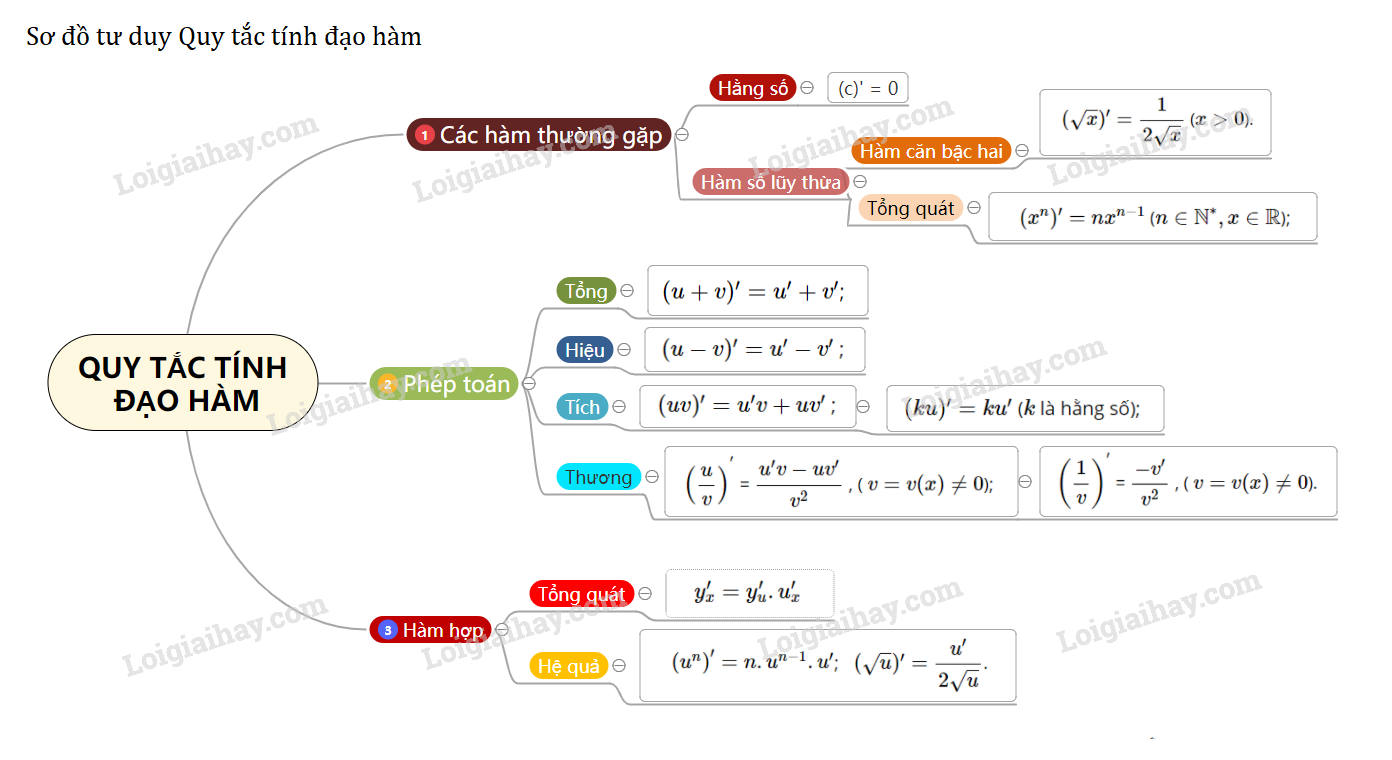
Lý thuyết Quy tắc tính đạo hàm


Tổng hợp lí thuyết về Quy tắc tính đạo hàm đầy đủ, ngắn gọn dễ hiểu

1. Công thức

  \((c)' = 0\)       ( \(c\) là hằng số);

  \((x^n)' = nx^{n-1}\) (\(n\in {\mathbb N}^*, x ∈\mathbb R\));

  \((\sqrt x)' =  \dfrac{1}{2\sqrt{x}}\) (\(x > 0\)).

2. Phép toán

\((u + v)' = u' + v' \);

\((u - v)' = u' - v'\) ;

\((uv)' = u'v + uv'\) ;

\((ku)' = ku'\) (\(k\) là hằng số);

\( \left ( \dfrac{u}{v} \right )^{^{'}}\) = \( \dfrac{u'v - uv'}{v^{2}}\) , ( \(v = v(x) ≠ 0\));

\( \left ( \dfrac{1}{v} \right )^{'}\) = \( \dfrac{-v'}{v^{2}}\) , ( \(v = v(x) ≠ 0\)).

3. Đạo hàm của hàm hợp

\[y_x' = y_u'.u_x'\]

Hệ quả: +)  \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\); 

             +) \((\sqrt u)' =  \dfrac{u'}{2\sqrt{u}}\).


Bình chọn:
3.7 trên 35 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store