Bài 5. Tiên đề Ơ-clit về đường thẳng song song

Bài 30 trang 108 SBT toán 7 tập 1

Giải bài 30 trang 108 sách bài tập toán 7 tập 1. Trên hình dưới, hai đường thẳng a, b song song với nhau, đường thẳng c cắt a tại A, cắt b tại B....

Đề bài

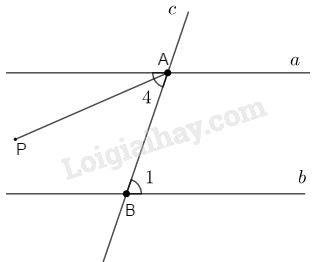
Trên hình dưới, hai đường thẳng \(a, b\) song song với nhau, đường thẳng \(c\) cắt \(a\) tại \(A\), cắt \(b\) tại \(B\).

a) Lấy một cặp góc so le trong (chẳng hạn cặp \({{\rm{A}}_4},{B_1})\) rồi đo xem hai góc đó có bằng nhau hay không?

b) Hãy lí luận vì sao \(\widehat {{A_4}} = \widehat {{B_1}}\) theo gợi ý sau:

Nếu \(\widehat {{{\rm{A}}_4}} \ne \widehat {{B_1}}\) thì qua \(A\) ta vẽ tia \(AP\) sao cho \(\widehat {PAB} = \widehat {{B_1}}\).

- Thế thì \(AP // b\), vì sao?

- Qua \(A\), vừa có \(a // b\), vừa có \(AP // b\), thì sao?

- Kết luận: Đường thẳng \(AP\) và đường thẳng \(a\) chỉ là một. Nói cách khác, \(\widehat {PAB} = \widehat {{A_4}}\), từ đó \(\widehat {{A_4}} = \widehat {{B_1}}\).

Phương pháp giải - Xem chi tiết

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Lời giải chi tiết

a) Lấy cặp góc so le trong là \(\widehat {{A_4}} ; \widehat {{B_1}}\)

Đo góc ta được: \(\widehat {{A_4}} = \widehat {{B_1}}\)

b) Nếu \(\widehat {{A_4}} \ne \widehat {{B_1}}\), thì qua \(A\) ta vẽ tia \(AP\) sao cho \(\widehat {PAB} = \widehat {{B_1}}\)

Mà 2 góc này ở vị trí so le trong nên \(AP // b\).

Khi đó, qua \(A\) ta vừa có \(a // b\), vừa có \(AP // b\), trái với tiên đề Ơclít về đường thẳng song song.

Vậy đường thẳng \(AP\) và đường thẳng \(a\) chỉ là một, hay \(\widehat {PAB} = \widehat {{A_4}}\) nghĩa là \(\widehat {{A_4}} = \widehat {{B_1}}\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 43 phiếu

Bài tiếp theo

Bài 5.1, 5.2, 5.3, 5.4 phần bài tập bổ sung trang 109, 110 SBT toán 7 tập 1
Giải bài 5.1, 5.2, 5.3, 5.4 phần bài tập bổ sung trang 109, 110 sách bài tập toán 7 tập 1. Biết rằng hai đường thẳng a, b song song với nhau. Một đường thẳng c cắt hai đường thẳng a, b ....
Bài 29 trang 108 SBT toán 7 tập 1
Giải bài 29 trang 108 sách bài tập toán 7 tập 1. Vẽ hai đường thẳng a, b sao cho a // b...
Bài 28 trang 108 SBT toán 7 tập 1
Giải bài 28 trang 108 sách bài tập toán 7 tập 1. Hãy điền vào chỗ trống (…) trong các phát biểu...
Bài 27 trang 108 SBT toán 7 tập 1
Giải bài 27 trang 108 sách bài tập toán 7 tập 1. Vẽ đường thẳng a và điểm A không thuộc a. Vẽ đường thẳng b đi qua A và song song với a. Vẽ được mấy đường thẳng b như thế?