-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 1.57 trang 44 SBT hình học 10
Giải bài 1.57 trang 44 sách bài tập hình học 10. Cho tam giác ABC. Gọi M, N , P là những điểm được xác định như sau...
Đề bài
Cho tam giác \(ABC\). Gọi \(M, N , P\) là những điểm được xác định như sau:\(\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NC} = 3\overrightarrow {NA} ,\)\(\overrightarrow {PA} = 3\overrightarrow {PB} \)
a) Chứng minh \(2\overrightarrow {OM} = 3\overrightarrow {OC} - \overrightarrow {OB} \) với mọi điểm \(O\).
b) Chứng minh hai tam giác \(ABC\) và \(MNP\) có cùng trọng tâm.
Phương pháp giải - Xem chi tiết
a) Xen điểm \(M\) vào các véc tơ trong đẳng thức và chứng minh.
b) Chứng minh nếu \(G\) là trọng tâm của \(\Delta ABC\) thì nó cũng là trọng tâm của \(\Delta MNP\).
Cụ thể, chứng minh \(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GP} = \overrightarrow 0 \).
Lời giải chi tiết
a) Ta có: \(3\overrightarrow {OC} - \overrightarrow {OB} \)\( = 3(\overrightarrow {OM} + \overrightarrow {MC} ) - (\overrightarrow {OM} + \overrightarrow {MB} )\)
\(\begin{array}{l}
= 3\overrightarrow {OM} + 3\overrightarrow {MC} - \overrightarrow {OM} - \overrightarrow {MB} \\
= \left( {3\overrightarrow {OM} - \overrightarrow {OM} } \right) + \left( {3\overrightarrow {MC} - \overrightarrow {MB} } \right)\\
= 2\overrightarrow {OM} + \left( {\overrightarrow {MB} - \overrightarrow {MB} } \right)\\
= 2\overrightarrow {OM} + \overrightarrow 0 \\
= 2\overrightarrow {OM}
\end{array}\)
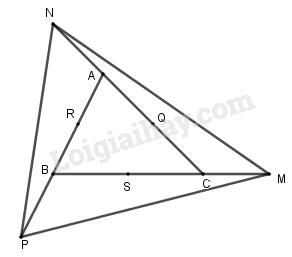
b) Gọi \(S, Q\) và \(R\) lần lượt là trung điểm của \(BC, CA\) và \(AB\).
\(\overrightarrow {MB} = 3\overrightarrow {MC} \Rightarrow \overrightarrow {CM} = \overrightarrow {SC} \); \(\overrightarrow {NC} = 3\overrightarrow {NA} \Rightarrow \overrightarrow {AN} = \overrightarrow {CQ} \)
\(\overrightarrow {PA} = 3\overrightarrow {PB} \Rightarrow \overrightarrow {BP} = \overrightarrow {RB} = \overrightarrow {QS} \)
Gọi \(G\) là trọng tâm của tam giác \(ABC\) thì \(\overrightarrow {GA} + \overrightarrow {BG} + \overrightarrow {GC} = \overrightarrow 0 \)
Ta có:
\(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GP} \)\( = \overrightarrow {GC} + \overrightarrow {CM} + \overrightarrow {GA} + \overrightarrow {AN} + \overrightarrow {GB} + \overrightarrow {BP} \) \( = \left( {\overrightarrow {GC} + \overrightarrow {GA} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {CM} + \overrightarrow {AN} + \overrightarrow {BP} } \right)\)
\( = \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {SC} + \overrightarrow {CQ} + \overrightarrow {QS} } \right)\)\( = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)
Vậy \(G\) là trọng tâm của tam giác \(MNP\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.58 trang 44 SBT hình học 10
- Bài 1.59 trang 44 SBT hình học 10
- Bài 1.60 trang 44 SBT hình học 10
- Bài 1.56 trang 43 SBT hình học 10
- Bài 1.55 trang 43 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
