-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 1.49 trang 43 SBT hình học 10
Giải bài 1.49 trang 43 sách bài tập hình học 10. Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N.
Đề bài
Cho hình bình hành \(ABCD\). Gọi \(E\) và \(F \) lần lượt là trung điểm của hai cạnh \(AB\) và \(CD\). Nối \(AF\) và \(CE\), hai đường thẳng này cắt đường chéo \(BD\) lần lượt tại \(M\) và \(N\). Chứng minh \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \).
Phương pháp giải - Xem chi tiết
Hai véc tơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết
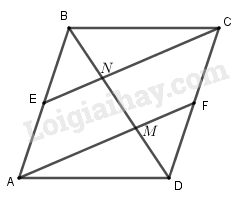
\(AECF\) là hình bình hành \( \Rightarrow \) \(EN // AM\)
\(E\) là trung điểm của \(AB\) \( \Rightarrow \) \(N\) là trung điểm của \(BM\), do đó \(MN = NB\).
Tương tự, \(M\) là trung điểm của \(DN\), do đó \(DM = MN\).
Vậy \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.50 trang 43 SBT hình học 10
- Bài 1.51 trang 43 SBT hình học 10
- Bài 1.52 trang 43 SBT hình học 10
- Bài 1.53 trang 43 SBT hình học 10
- Bài 1.54 trang 43 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
