Câu hỏi 4 trang 22 SGK Hình học 11

• Câu hỏi 5 trang 23 SGK Hình học 11

  Cho hình chữ nhật ABCD...

• Bài 1 trang 23 SGK Hình học 11

  Trong mặt phẳng Oxy cho các điểm A(-3;2), B(-4;5) và C(-1;3)

• Bài 2 trang 24 SGK Hình học 11

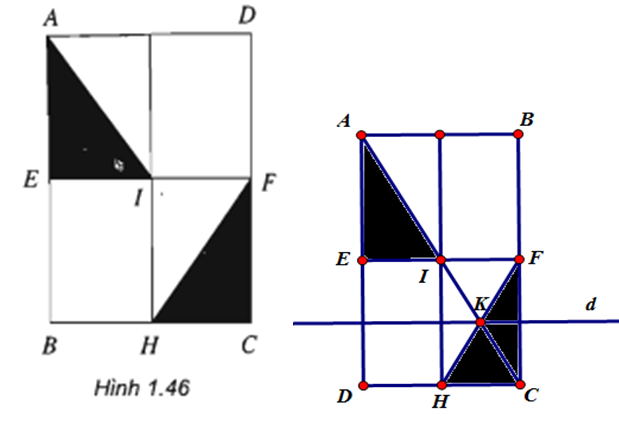
  Cho hình chữ nhật ABCD. Gọi E, F, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.

• Bài 3 trang 24 SGK Hình học 11

  Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A'B'C' thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A'B'C'

• Câu hỏi 3 trang 21 SGK Hình học 11

  Gọi A’, B’ lần lượt là ảnh của A, B qua phép dời hình F. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F(M) là trung điểm của A’B’....

• Câu hỏi 2 trang 21 SGK Hình học 11

  Hãy chứng minh tính chất 1....

• Câu hỏi 1 trang 20 SGK Hình học 11

  Cho hình vuông ABCD...

• Lý thuyết khái niệm về phép dời hình và hai hình bằng nhau

>> Xem thêm