Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học Bài 1. Phương pháp quy nạp toán học

Bài 5 trang 83 SGK Đại số và Giải tích 11


Chứng minh rằng

Đề bài

Chứng minh rằng số đường chéo của một đa giác lồi \(n\) cạnh là \(\displaystyle {{n(n - 3)} \over 2}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Ta chứng minh khẳng định đúng với mọi \(n \in{\mathbb N}^*\), \(n ≥ 4\).

Sử dụng phương pháp quy nạp toán học để chứng minh.

Quảng cáo

Lộ trình SUN 2025

Lời giải chi tiết

Kí hiệu số đường chéo của đa giác \(n\) cạnh là \(C_n\).

Ta chứng minh \(\displaystyle C_n = {{n(n - 3)} \over 2}\) (1) với mọi \(n \in{\mathbb N}^*\), \(n ≥ 4\).

*) Với \(n = 4\), ta có tứ giác nên nó có 2 đường chéo.

Mặt khác \(\displaystyle {{4(4 - 3)} \over 2} = 2\) nên (1) đúng với \(n = 4\).

Vậy khẳng định đúng với \(n= 4\).

*) Giả sử (1) đúng với \(n = k ≥ 4\), tức là \(C_k = \displaystyle {{k(k - 3)} \over 2}\)

*) Ta phải chứng minh (1) đúng với \(n = k + 1\).
Tức là \(C_{k+1}=\displaystyle {{(k + 1)((k + 1) - 3)} \over 2}\)
Xét đa giác lồi \(k + 1\) cạnh
Đa giác \(k\) cạnh \(A_1A_2...A_k\) có \(\displaystyle {{k(k - 3)} \over 2}\) đường chéo (giả thiết quy nạp).
Nối \(A_{k+1}\) với các đỉnh \(A_2,...,A_{k-1}\), ta được thêm \(k -2\) đường chéo.
Ngoài ra \(A_1A_k\) cũng là một đường chéo.

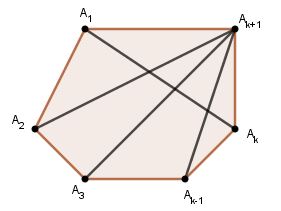
Vậy số đường chéo của đa giác \(k + 1\) cạnh là

\(\displaystyle {{k(k - 3)} \over 2}+ k - 2 + 1\)

\( = \dfrac{{{k^2} - 3k}}{2} + k - 1 \)

\(= \dfrac{{{k^2} - 3k + 2k - 2}}{2}\)

\(\displaystyle ={{{k^2} - k - 2} \over 2} \)

\( = \dfrac{{\left( {k + 1} \right)\left( {k - 2} \right)}}{2}\)

\(\displaystyle = {{(k + 1)((k + 1) - 3)} \over 2}\)

Như vậy, khẳng định cũng đúng với đa giác \(k + 1\) cạnh

Vậy bài toán đã được chứng minh.

Chú ý:

Trên đây là cách chứng minh bằng quy nạp, các em có thể dễ dàng chứng minhcông thức đó bằng kiến thức chương 2 như sau:

Cách 2: Đa giác lồi \(n\) cạnh có \(n\) đỉnh.

Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.

⇒ Tổng số cạnh và đường chéo của đa giác bằng:

\(C_n^2 = \dfrac{{n!}}{{2!\left( {n - 2} \right)!}}\)\( = \dfrac{{n\left( {n - 1} \right)\left( {n - 2} \right)!}}{{2\left( {n - 2} \right)!}} = \dfrac{{n\left( {n - 1} \right)}}{2}\)

⇒ Số đường chéo của đa giác lồi có \(n\) cạnh là:

\(\dfrac{{n\left( {n - 1} \right)}}{2} - n = \dfrac{{{n^2} - n - 2n}}{2}\)\( = \dfrac{{{n^2} - 3n}}{2} = \dfrac{{n\left( {n - 3} \right)}}{2}\)

Vậy ta có đpcm.

Loigiaihay.com


Bình chọn:
4.7 trên 13 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua