-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11
-
HÌNH HỌC - TOÁN 11
-
CHƯƠNG I. PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
-
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
- Bài 1. Đại cương về đường thẳng và mặt phẳng
- Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3. Đường thẳng và mặt phẳng song song
- Bài 4. Hai mặt phẳng song song
- Bài 5. Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương II - Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
-
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
-
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
-
-
Câu hỏi tự luyện Toán 11
-
TẢI 50 ĐỀ KIỂM TRA 15 PHÚT TOÁN 11
-
TẢI 30 ĐỀ KIỂM TRA 1 TIẾT TOÁN 11
-
TẢI 5 ĐỀ THI GIỮA KÌ 1 TOÁN 11
-
TẢI 25 ĐỀ THI HỌC KÌ 1 TOÁN 11
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 11
-
TẢI 20 ĐỀ THI HỌC KÌ 2 TOÁN 11
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Bài 2. Hai đường thẳng chéo nhau và hai đường thẳng son..
Bài 3 trang 60 SGK Hình học 11
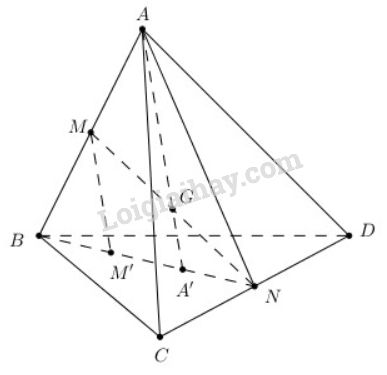
Cho tứ diện ABCD. Gọi M, N lần lượt là trung đểm của các cạnh AB, CD và G là trung điểm của đoạn MN
Đề bài
Cho tứ diện \(ABCD\). Gọi \(M, N\) lần lượt là trung đểm của các cạnh \(AB, CD\) và \(G\) là trung điểm của đoạn \(MN\)
a) Tìm giao điểm \(A'\) của đường thẳng \(AG\) và mặt phẳng \((BCD)\)
b) Qua \(M\) kẻ đường thẳng \(Mx\) song song với \(AA'\) và \(Mx\) cắt \((BCD)\) tại \(M'\). Chứng minh \(B, M', A'\) thẳng hàng và \(BM' = M'A' = A'N\).
c) Chứng minh \(GA = 3 GA'\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Trong \((ABN)\): Gọi \(A'=AG \cap BN\).
b) Sử dụng định lí đường trung bình của tam giác.
c) Sử dụng tính chất đường trung bình của tam giác.
Quảng cáo
Lời giải chi tiết
a) Có: \(MN \subset \left( {ABN} \right)\)
\(\begin{array}{*{20}{l}}
{ \Rightarrow {\rm{ }}G \in \left( {ABN} \right)}\\
{ \Rightarrow {\rm{ }}AG \subset \left( {ABN} \right).}
\end{array}\)
Trong \((ABN)\): Gọi \(A'=AG \cap BN\)
\( \Rightarrow A' \in BN \subset (BCD)\).
\( \Rightarrow A' \in (BCD) \Rightarrow A' = AG \cap (BCD)\)
b) Ta có: \(\left\{ \begin{array}{l}MM'//AA'\\AA' \subset \left( {ABN} \right)\\M \in AB \subset \left( {ABN} \right)\end{array} \right. \) \(\Rightarrow MM' \subset \left( {ABN} \right)\)
Suy ra \(\left\{ \begin{array}{l}M' \in \left( {ABN} \right)\\M' \in \left( {BCD} \right)\end{array} \right.\)
\( \Rightarrow M' \in \left( {ABN} \right) \cap \left( {BCD} \right) = BN\).
Mà \(A'\) cũng thuộc \(BN\) nên \(M',A',B\) thẳng hàng (cùng nằm trên \(BN\)).
*) Xét tam giác \(NMM'\) có:
+) \(G\) là trung điểm của \(NM\).
+) \(GA'//MM'\)
\(\Rightarrow A'\) là trung điểm của \(NM'\)
Xét tam giác \(BAA'\) có:
+) \(M \) là trung điểm của \(AB\)
+) \(MM'//AA'\)
\(\Rightarrow M'\) là trung điểm của \(BA'\)
Do đó: \(BM'=M'A'=A'N\).
c) Ta có \(\displaystyle MM'={1\over 2} AA'\)
\( \Rightarrow GA' = \frac{1}{2}MM' = \frac{1}{2}.\frac{1}{2}AA' = \frac{1}{4}AA' \)
\(\Rightarrow GA = AA' - GA' \) \(= AA' - \frac{1}{4}AA' = \frac{3}{4}AA'\)
\( \Rightarrow \dfrac{{GA'}}{{GA}} = \dfrac{{\dfrac{1}{4}AA'}}{{\dfrac{3}{4}AA'}} = \dfrac{1}{3} \) \(\Rightarrow GA = 3GA'\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 2 trang 59 SGK Hình học 11
- Bài 1 trang 59 SGK Hình học 11
- Câu hỏi 3 trang 57 SGK Hình học 11
- Câu hỏi 2 trang 56 SGK Hình học 11
- Câu hỏi 1 trang 55 SGK Hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
