Câu hỏi 5 trang 10 SGK Hình học 11

Đề bài

Chọn hệ tọa độ \(Oxy\) sao cho trục \(Ox\) trùng với trục đối xứng, rồi dùng biểu thức tọa độ của phép đối xứng qua trục \(Ox\) để chứng minh tính chất 1.

Video hướng dẫn giải

Lời giải chi tiết

Gọi \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\)

Xét phép đối xứng qua trục \(Ox\) thì \(A, B\) biến thành \(A'\left( {{x_A}; - {y_A}} \right),B'\left( {{x_B}; - {y_B}} \right)\)

Khi đó:

\(\begin{array}{l}
AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \\
A'B' = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( { - {y_B} + {y_A}} \right)}^2}} \\
= \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \\
= AB\\
\Rightarrow A'B' = AB \Rightarrow dpcm
\end{array}\)

Chú ý:

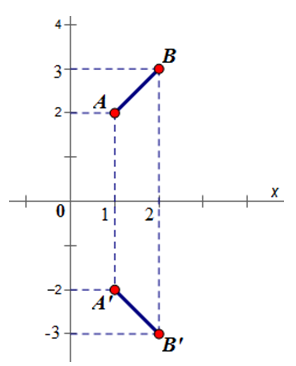
Trực quan các em có thể lấy hai điểm \(A, B\) cụ thể như sau:

Lấy ảnh \(A',B'\) của hai điểm \(A(1; 2)\) và \(B(2; 3)\) qua phép đối xứng trục \(Ox\)

Dùng biểu thức tọa độ của phép đối xứng qua trục \(Ox\), ta có:

\(A'(1;-2), B'(2;-3)\)

\(\eqalign{
& AB = \sqrt {{{(2 - 1)}^2} + {{(3 - 2)}^2}} \cr &= \sqrt {{1^2} + {1^2}} = \sqrt 2 \cr
& A'B' = \sqrt {{{(2 - 1)}^2} + {{( - 3 - ( - 2))}^2}} \cr &= \sqrt {{1^2} + {{( - 1)}^2}} = \sqrt 2 \cr} \)

\(⇒ A'B' = AB\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Câu hỏi 6 trang 11 SGK Hình học 11
Trong những chữ cái dưới đây, chữ nào là hình có trục đối xứng?...
Bài 1 trang 11 SGK Hình học 11
Trong mặt phẳng Oxy cho hai điểm A (1;-2) và B (3;1). Tìm ảnh của A, b và đường thẳng AB qua phép đối xứng trục Ox
Bài 2 trang 11 SGK Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x-y+2=0. Viết phương trình của đường thẳng d' là ảnh của d qua phép đối xứng trục Oy.
Bài 3 trang 11 SGK Hình học 11
Trong các chữ cái sau, chữ nào có trục đối xứng
Câu hỏi 4 trang 10 SGK Hình học 11
Tìm ảnh của các điểm A(1; 2), B(5; 0) qua phép đối xứng trục Oy....
Câu hỏi 3 trang 9 SGK Hình học 11
Tìm ảnh của các điểm A(1; 2), B(0; -5) qua phép đối xứng trục qua trục Ox...
Câu hỏi 2 trang 9 SGK Hình học 11
Chứng minh nhận xét 2....
Câu hỏi 1 trang 9 SGK Hình học 11
Cho hình thoi ABCD (h.1.12)...
Lý thuyết Phép đối xứng trục