Bài 6 trang 126 SGK Hình học 11

a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau BD' và B'C.

Đề bài

Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\).

a) Hãy xác định đường vuông góc chung của hai đường thẳng chéo nhau \(BD'\) và \(B'C\).

b)Tính khoảng cách của hai đường thẳng \(BD'\) và \(B'C\)

Video hướng dẫn giải

Lời giải chi tiết

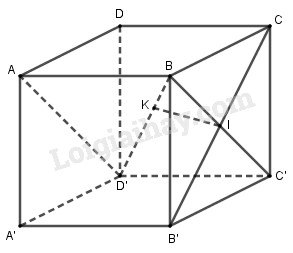
a) \(AB ⊥ (BCC’B’) ⇒ AB ⊥ B’C\)

\(BCC’B’\) là hình vuông có \(BC’ ⊥ B’C\)

\(⇒ B’C ⊥ (ABC’D’)\)

Trong mặt phẳng \((ABC’D’)\), kẻ \(IK ⊥ BD’\).

Vì \(B’C ⊥ (ABC’D’) ⇒ B’C ⊥ IK\)

Kết hợp với \(IK ⊥ BD’ \) \( ⇒ IK\) là đường vuông góc chung của \(B’C\) và \(BD’\)

b) Ta có: \(d\left( {B'C,BD'} \right) = IK\)

\(C'B = \sqrt {C{B^2} + B'{B^2}} \) \(= \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)

\(D'B = \sqrt {C'{B^2} + C'D{'^2}} \) \( = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)

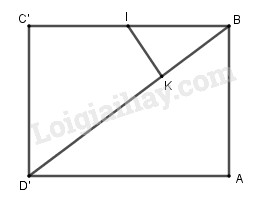
Xét \(∆BIK\) và \(∆BD’C’\) có:

B chung

\(\widehat {BC'D'} = \widehat {BKI} = {90^0}\)

Suy ra \(∆BIK \backsim ∆BD’C’\) (g-g)

\(\eqalign{
& \Rightarrow {{IK} \over {D'C'}} = {{BI} \over {B{\rm{D}}'}} \cr
& \Rightarrow IK = {{BI.D'C'} \over {B{\rm{D}}'}} \cr} \).

Mà \(BI = \dfrac{1}{2}BC' = \dfrac{{a\sqrt 2 }}{2}\) nên:

\(IK = \dfrac{{\frac{{a\sqrt 2 }}{2}.a}}{{a\sqrt 3 }} = \dfrac{{a\sqrt 6 }}{6}\)

Vậy \(d\left( {B'C,BD'} \right) = \dfrac{{a\sqrt 6 }}{6} \)

loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 7 phiếu

Bài 7 trang 126 SGK Hình học 11
Giải bài 7 trang 126 SGK Hình học 11. Cho hình thang ABCD vuông tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S.
Bài 5 trang 126 SGK Hình học 11
Giải bài 5 trang 126 SGK Hình học 11. Cho hình lập phương ABCD.A'B'C'D' có E và F lần lượt là trung điểm của các cạnh AB và Đ'.
Bài 4 trang 126 SGK Hình học 11
Giải bài 4 trang 126 SGK Hình học 11. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’ có E, F, M và N lần lượt là trung điểm của AC, BD, AC’ và BD’. Chứng minh MN = EF.
Bài 3 trang 126 SGK Hình học 11
Giải bài 3 trang 126 SGK Hình học 11. Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn.
Bài 2 trang 125 SGK Hình học 11
a) Tìm phép vị tự F biến A, B, C tương ứng thành A', B',C'
Bài 1 trang 125 SGK Hình học 11
Giải bài 1 trang 125 SGK Hình học 11. Trong mặt phẳng tọa độ Oxy, cho các điểm A (1; 1), B(0; 3), C(2; 4) .Xác định ảnh của tam giác ABC qua các phép biến hình sau.