 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11
Bài 3 trang 126 SGK Hình học 11
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn.
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\) là đáy lớn. Gọi \(M\) là trung điểm của đoạn \(AB\), \(E\) là giao điểm của hai cạnh của hình thang \(ABCD\) và \(G\) là trọng tâm của tam giác \(ECD\).
a) Chứng minh rằng bốn điểm \(S, E, M, G\) cùng thuộc một mặt phẳng \((α)\) và mặt phẳng này cắt cả hai mặt phẳng \((SAC)\) và \((SBD)\) theo cùng một giao tuyến \(d\).
b) Xác định giao tuyến của hai mặt phẳng \((SAD)\) và \((SBC)\).
c) Lấy một điểm \(K\) trên đoạn \(SE\) và gọi \(C'= SC ∩KB, D'=SD ∩ KA\). Chứng minh rằng hai giao điểm của \(AC'\) và \(BD'\) thuộc đường thẳng \(d\) nói trên.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh mặt phẳng \((\alpha)\) chính là mặt phẳng \((SEM)\).
b) Tìm hai điểm chung của hai mặt phẳng \((SAD)\) và \((SBC)\).
c) Gọi \(I = AC' \cap BD'\), chứng minh \(AC' \subset \left( {SAC} \right);\,\,BD' \subset \left( {SBD} \right) \Rightarrow I\) là điểm chung của hai mặt phẳng (SAC) và (SBD).
Lời giải chi tiết
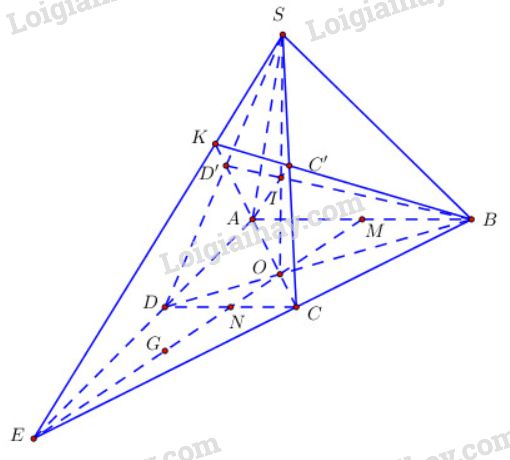
a) Gọi \(O\) là giao điểm của \(AC\) và \(DB\); \(N\) là giao của \(EM\) và \(DC\).
\(M\) là trung điểm của \(AB\) nên \(N\) là trung điểm của \(DC\) (vì \(ABCD\) là hình thang)
Mà G là trọng tâm tam giác EDC nên \(G \in EN\)
\( \Rightarrow G \in \left( {SEM} \right)\) hay các điểm \(S, E, G, M\) cùng thuộc mặt phẳng \((\alpha)\) chính là mặt phẳng \((SEM)\)
Ta dễ thấy \(\left\{ \begin{array}{l}\left( {SEM} \right) \cap \left( {SAC} \right) = SO\\\left( {SEM} \right) \cap \left( {SBD} \right) = SO\end{array} \right.\)
b) \(E = AD \cap BC \Rightarrow E \in AD \Rightarrow E \in (SAD)\)
\(E ∈ BC ⇒ E ∈ (SBC)\)
Vậy \(E\) là một điểm chung của hai mặt phẳng \((SAD)\) và \((SBC)\)
\(S\) là điểm chung của hai mặt phẳng \((SAD)\) và \((SBC)\)
\( \Rightarrow \left( {SAD} \right) \cap \left( {SBC} \right) = SE\)
c) \(C' = SC \cap KB \Rightarrow C' \in SC \Rightarrow C' \in \left( {SAC} \right)\)\( \Rightarrow AC' \subset \left( {SAC} \right)\)
Tương tự ta có: \(BD' ∈ (SDB)\)
Hai đường thẳng \(AC’\) và \(BD’\) cùng thuộc mặt phẳng \((ABK)\), giả sử \(I = AC' \cap BD'\)
\(I ∈ AC’ \subset (SAC); I ∈ BD’ \subset (SDB)\)
\(⇒ I\) là điểm chung của hai mặt phẳng \((SAC)\) và \((SDB)\) hay \(I ∈ d\) là giao tuyến của hai mặt phẳng (SAC) và (SBD).
Loigiaihay.com












Danh sách bình luận