Giải SBT toán hình học và giải tích 12 nâng cao Ôn tập cuối năm Giải tích

Câu 5 trang 210 sách bài tập Giải tích 12 Nâng cao


Cho hàm số

Lựa chọn câu để xem lời giải nhanh hơn

Cho hàm số

            \(f\left( x \right) = {{{x^2} - 2x} \over {x - 1}}\)

LG a

Khảo sát sự biến thiên và vẽ đồ thị  (C) của hàm số f

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\)

\(\begin{array}{l}y = \dfrac{{{x^2} - 2x}}{{x - 1}} = x - 1 - \dfrac{1}{{x - 1}}\\y' = 1 + \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} > 0\end{array}\)

\( \Rightarrow \)Hàm số đồng biến trên  \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x - 1 - \dfrac{1}{{x - 1}}} \right) =  - \infty \\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x - 1 - \dfrac{1}{{x - 1}}} \right) =  + \infty \end{array}\)

\(\mathop {\lim }\limits_{x \to  + \infty } \left( {y - x + 1} \right) = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{ - 1}}{{x - 1}} = 0\)

\( \Rightarrow x = 1;y = x - 1\) lần lượt là tiệm cận đứng và tiệm cận xiên của đồ thị

Bảng biến thiên:

 

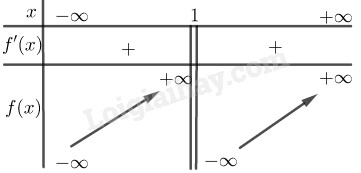
Đồ thị:

 

Quảng cáo

Lộ trình SUN 2025

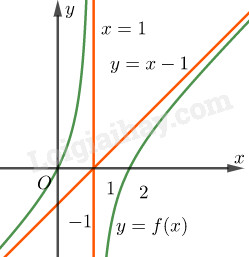
LG b

Từ đồ thị (C) suy ra cách vẽ đồ thị hàm số

            \(g\left( x \right) = {{{x^2} - 2\left| x \right|} \over {\left| x \right| - 1}}\)

Lời giải chi tiết:

g là một hàm số chẵn nên đồ thị \(({C_1})\) của đồ thị đối xứng qua trục tung. Với \(x \ge 0,\) ta có

            \(g\left( x \right) = {{{x^2} - 2x} \over {x - 1}} = f\left( x \right)\)

Do đó, muốn có đồ thị \(\left( {{C_1}} \right)\) của hàm số g ta bỏ đi phần đường cong (C) nằm bên trái trục tung, giữ lại phần của đường cong (C) nằm bên phải trục tung (ứng với các giá trị \(x \ge 0,x \ne 1\)) và bổ xung thêm hình đối xứng của phần đường cong này qua trục tung.

LG c

Với các giá trị nào của m thì phương trình

             \({x^2} - 2\left| x \right| = m\left( {\left| x \right| - 1} \right)\)

có bốn nghiệm thực phân biệt ?

Lời giải chi tiết:

\(m > 0\)

Phương trình đã cho tương đương với phương trình

            \({{{x^2} - 2\left| x \right|} \over {\left| x \right| - 1}} = m\)

Số nghiệm của phương trình đã cho bằng số giao điểm \(\left( {{C_1}} \right)\) và đường thẳng \(y = m\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua