-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Câu 1 trang 209 sách bài tập Giải tích 12 Nâng cao
Cho hàm số:
Cho hàm số:
\(f\left( x \right) = 1 + x + {{{x^2}} \over 2} - {e^x}\)
LG a
Chứng minh rằng \(f'\left( x \right) < 0\) với mọi x < 0
Lời giải chi tiết:
\(f'\left( x \right) = 1 + x - {e^x},f''\left( x \right) = 1 - {e^x}\)
\(f''\left( x \right) = 0 \Leftrightarrow x = 0\)
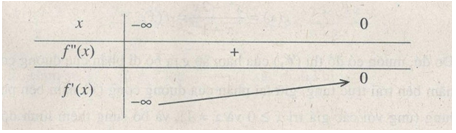
Dựa vào bảng biến thiên, ta có \(f'\left( x \right) > 0\) với mọi x < 0.
LG b
Chứng minh bất đẳng thức
\(1 + x < {e^x} + x + {{{x^2}} \over 2}\) với mọi x < 0
Lời giải chi tiết:
Từ a) suy ra f nghịch biến trên nửa khoảng\(\left( { - \infty ;0} \right]\). Do đó
\(f(x) > f(0)\) , với mọi x < 0,
Hay \(1 + x + {{{x^2}} \over 2} - {e^x} > 0\) với mọi x < 0
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 2 trang 209 sách bài tập Giải tích 12 Nâng cao
- Câu 3 trang 209 sách bài tập Giải tích 12 Nâng cao
- Câu 4 trang 210 sách bài tập Giải tích 12 Nâng cao
- Câu 5 trang 210 sách bài tập Giải tích 12 Nâng cao
- Câu 6 trang 210 sách bài tập Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
