Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Ôn tập chương III - Phương pháp toạ độ trong không ..
Các dạng toán về mặt cầu và mặt phẳng
Các dạng toán về mặt cầu và mặt phẳng
1. Kiến thức cần nhớ
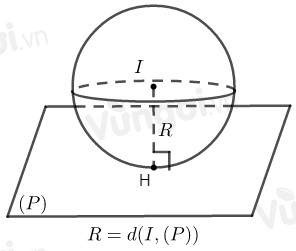
Cho mặt phẳng \(\left( P \right)\) và mặt cầu \(\left( S \right)\) tâm \(I\) bán kính \(R\). Khi đó:
- \(\left( S \right) \cap \left( P \right) = \emptyset \Leftrightarrow d\left( {I,\left( P \right)} \right) > R.\)
- \(\left( S \right) \cap \left( P \right) = \left\{ H \right\} \Leftrightarrow d\left( {I,\left( P \right)} \right) = R.\)
ở đó, \(H\) là tiếp điểm, \(\left( P \right)\) là tiếp diện và \(OH \bot \left( P \right)\) tại \(H.\)
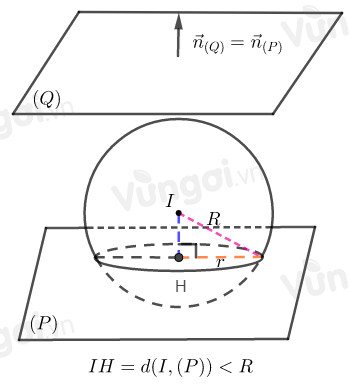
- \(\left( S \right) \cap \left( P \right) = C\left( {H;r} \right) \Leftrightarrow d\left( {I,\left( P \right)} \right) < R.\)
ở đó : với \(H\) là hình chiếu của \(I\) trên \(\left( P \right)\).
Đặc biệt: \(d\left( {I,\left( P \right)} \right) = 0\) hay \(\left( P \right)\) đi qua \(I\) thì \(\left( S \right) \cap \left( P \right) = C\left( {I;R} \right).\)
\(C\left( {I;R} \right)\) được gọi là đường tròn lớn, \(\left( P \right)\) là mặt phẳng kính.
2. Một số dạng toán thường gặp
Dạng 1: Viết phương trình mặt cầu tiếp xúc hoặc cắt mặt phẳng cho trước.
Phương pháp:
- Bước 1: Tính bán kính mặt cầu dựa vào các điều kiện bài cho:
+ Tiếp xúc mặt phẳng nếu \(d\left( {I,\left( P \right)} \right) = R\)
+ Cắt mặt phẳng theo giao tuyến và đường tròn bán kính \(r\) thì \(R^2 = {r^2} + {d^2}\left( {I,\left( P \right)} \right)\)
- Bước 2: Viết phương trình mặt cầu biết tâm và bán kính.
Ví dụ:
1) Viết phương trình mặt cầu có tâm I(1; -2; 0) và tiếp xúc với mặt phẳng (P): x + 2x + 2z – 5 = 0.
Giải:
Khoảng cách từ I đến mặt phẳng (P) là:
\(d\left( {I,(P)} \right) = \frac{{\left| {1 + 2.( - 2) + 2.0 - 5} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} }} = \frac{8}{3}\).
Do (P) tiếp xúc với mặt cầu (S) nên bán kính mặt cầu \(R = d\left( {I,(P)} \right) = \frac{8}{3}\).
Khi đó, phương trình mặt cầu có tâm I(1; -2; 0) và tiếp xúc với (P) là:
\({(x - 1)^2} + {(y + 2)^2} + {z^2} = \frac{{64}}{9}\).
2) Viết phương trình mặt cầu có tâm I(3; -4; 2) và tiếp xúc với mặt phẳng (Oxy).
Giải:
Mặt phẳng (Oxy) có phương trình là z = 0.
Khoảng cách từ I đến mặt phẳng (Oxy) là:
\(d\left( {I,(Oxy)} \right) = \frac{{\left| {0.3 + 0.( - 4) + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2\).
Do (Oxy) tiếp xúc với mặt cầu (S) nên bán kính mặt cầu \(R = d\left( {I,(Oxy)} \right) = 2\).
Khi đó, phương trình mặt cầu có tâm I(3; -4; 2) và tiếp xúc với (Oxy) là:
\({(x - 3)^2} + {(y + 4)^2} + {(z - 2)^2} = 4\).
Dạng 2: Viết phương trình mặt phẳng \((P)\) tiếp xúc, giao với mặt cầu cho trước.
Phương pháp:
- Bước 1: Tìm VTPT của mặt phẳng \((P)\) dựa vào điều kiện bài cho.
+ Tiếp xúc mặt cầu tại điểm \(H\) thì \(\overrightarrow {{n_P}} = \overrightarrow {IH} \)
+ Trường hợp \((P)\) song song với mặt phẳng \((Q):ax+by+cz+d=0\) (\(a,b,c,d\) là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính \(r\) thì \(\overrightarrow {{n_P}} = \overrightarrow {{n_Q}} \) tức là \((P):ax+by+cz+d'=0\).
và \(d\left( {I,\left( P \right)} \right) = \sqrt {{R^2} - {r^2}} \).
- Bước 2: Viết phương trình mặt phẳng.
+ Tiếp xúc mặt cầu tại điểm \(H\): Xác định điểm \(H\) rồi lập phương trình mặt phẳng.
+ Trường hợp \((P)\) song song với mặt phẳng \((Q):ax+by+cz+d=0\) (\(a,b,c,d\) là các số cho trước) và cắt mặt cầu theo đường tròn có bán kính \(r\):
Sử dụng \(d\left( {I,\left( P \right)} \right) = \sqrt {{R^2} - {r^2}} \) để tìm d'.
Ví dụ:
Trong không gian hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng (Q): $x + 2y - 2z + 1 = 0$ và tiếp xúc với mặt cầu $(S): x^2 + y^2 + z^2 + 2x - 4y - 2z - 3 = 0$.
Giải:
Mặt cầu (S) có tâm $I (-1; 2; 1)$ và bán kính $R = 3$.
Do (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:
$x + 2y - 2z + D = 0 \quad (D \neq 1)$.
Vì (P) tiếp xúc với mặt cầu (S) nên $d(I; (P)) = R = 3$
$\Leftrightarrow \frac{| -1 + 2.2 - 2.1 + D |}{\sqrt{1^2 + 2^2 + (-2)^2}} = 3$
$\Leftrightarrow |1 + D| = 9 \Leftrightarrow D = -10$.
Vậy có 2 mặt phẳng thỏa mãn yêu cầu đề bài là:
+) $x + 2y - 2z + 8 = 0$.
+) $x + 2y - 2z - 10 = 0$.
Bình luận
Chia sẻ
- Các dạng toán về mặt cầu và đường thẳng
- Phương trình mặt cầu trong không gian
- Các dạng toán về đường thẳng và mặt phẳng
- Bài 15 trang 97 SGK Hình học 12
- Bài 14 trang 97 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
Danh sách bình luận