Câu hỏi:
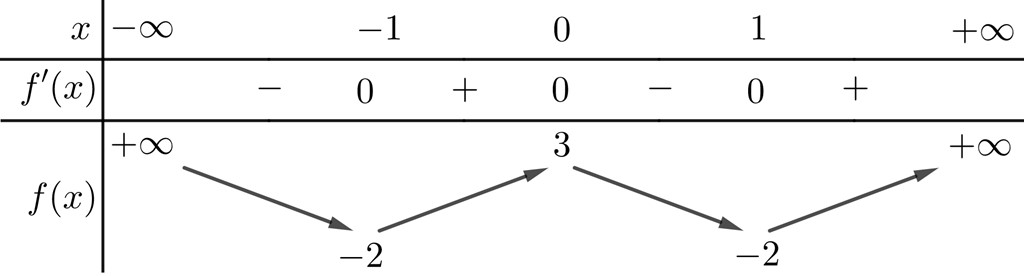
Cho hàm số \(y = {\rm{ }}f\left( x \right)\) có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?
- A
Hàm số y = f(x) đồng biến trên \(\left( { - \infty \,;\; - 1} \right)\)
- A
Hàm số y = f(x) nghịch biến trên \(\left( {\,1\;;\, + \infty } \right)\)
- C
Hàm số y = f(x) đồng biến trên \(\left( { - 1\,;\;1} \right)\)
- D
Hàm số y = f(x) nghịch biến trên \(\left( {0\,;\;1} \right)\)
Câu hỏi:
Để trang trí cho một căn phòng trong ngôi nhà, ông An vẽ lên tường một hình như sau: trên mỗi cạnh của hình lục giác đều có cạnh bằng 4dm có một cánh hoa hình Parabol, đỉnh của Parabol cách cạnh 5dm và nẳm phía ngoài hình lục giác như hình vẽ dưới. Hãy tính diện tích của hình nói trên (kể cả hình lục giác đều) để mua sơn trang trí cho phù hợp.

Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Cho số phức \(z\) thỏa mãn \(|z + 4 + i| + |z - 4 - 3i| = 4\sqrt 5 \). Tìm giá trị lớn nhất của biểu thức \(P = |z + 6 - 4i|\).
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Trong không gian Oxyz, viết phương trình của mặt phẳng \((\beta )\) vuông góc với mặt phẳng \((\alpha ):2x - 3y + z - 2 = 0\) đồng thời chứa đường thẳng \(d:\frac{x}{{ - 1}} = \frac{{y + 1}}{2} = \frac{{z - 2}}{{ - 1}}\).
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Tìm \(\int x \ln (x - 1) \cdot dx\).
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Trong không gian với hệ trục toạ độ Oxyz, tính khoảng cách từ điểm \(M(1;2; - 3)\) đến măt phẳng \((P):x + 2y - 2z - 2 = 0\).
- A \(d(M,(P)) = 1\).
- A \(d(M,(P)) = \frac{1}{3}\).
- C \(d(M,(P)) = 3\).
- D \(d(M,(P)) = \frac{{11}}{3}\).
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Tìm số phức nghịch đảo của số phức \(z = ai\).
- A \(\frac{1}{a}i\).
- A \(\frac{1}{a}\).
- C \( - ai\).
- D \( - \frac{1}{a}i\)
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Biết \(\int_0^{\frac{\pi }{2}} {(x - 1)} \cos xdx = \frac{{\pi - a}}{b},\left( {a,b \in {\mathbb{N}^*}} \right)\). Tính \({a^2} + 2b\).
- A 18 .
- A 6 .
- C 20 .
- D 8 .
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Nếu \(F(x)\) là một nguyên hàm của hàm số \(f(x) = \frac{1}{{x - 1}}\) và \(F(2) = 1\) thì \(F(3)\) bằng
- A \(F(3) = \frac{1}{2}\).
- A \(F(3) = \ln 2\).
- C \(F(3) = \ln 2 + 1\).
- D \(F(3) = \ln \frac{3}{2}\).
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn
Câu hỏi:
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;2} \right),B\left( {3;0;2} \right)\). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là
- A \(x - y - z + 1 = 0\)
- A \(x - y - 1 = 0\)
- C \(x + y - z - 1 = 0\)
- D \(x + y - 3 = 0\)
Giải đề thi học kì 2 toán lớp 12 năm 2020 - 2021 trường THPT Trần Quốc Tuấn






