Bài 2 trang 63 SGK Hình học lớp 11

Cho tứ diện ABCD. Trên cạnh AB lấy một điểm M. Cho (α) là mặt phẳng qua M, song song với hai đường thẳng AC và BD

Đề bài

Cho tứ diện \(ABCD\). Trên cạnh \(AB\) lấy một điểm \(M\). Cho \((α)\) là mặt phẳng qua \(M\), song song với hai đường thẳng \(AC\) và \(BD\)

a) Tìm giao tuyến của \((α)\) với các mặt tứ diện

b) Thiết diện của tứ diện cắt bởi mặt phẳng \((α)\) là hình gì?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Vận dụng định lí 2:

Cho đường thẳng \(a\) song song với mặt phẳng \(\alpha\). Nếu mặt phẳng \(\beta\) chứa \(a\) và cắt \(\alpha\) theo giao tuyến \(b\) thì \(b\) song song với \(a\).

Lời giải chi tiết

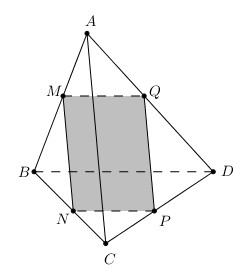
a) Ta có:

+ \((α) // AC\)

⇒ Giao tuyến của \((α)\) và \((ABC)\) là đường thẳng song song với \(AC.\)

Mà \(M ∈ (ABC) ∩ (α).\)

\(⇒ (ABC) ∩ (α) = MN\) là đường thẳng qua \(M,\) song song với \(AC (N ∈ BC).\)

+ Tương tự \((α) ∩ (ABD) = MQ\) là đường thẳng qua \(M\) song song với \(BD (Q ∈ AD).\)

+ \((α) ∩ (BCD) = NP\) là đường thẳng qua \(N\) song song với \(BD (P ∈ CD).\)

+ \((α) ∩ (ACD) = QP.\)

b) Ta có:

\(\left\{ \begin{array}{l}
\left( \alpha \right) \cap \left( {ABD} \right) = MQ\\
\left( \alpha \right) \cap \left( {ABC} \right) = MN\\
\left( \alpha \right) \cap \left( {ACD} \right) = PQ\\
\left( \alpha \right) \cap \left( {BCD} \right) = PN
\end{array} \right.\) nên thiết diện là tứ giác \(MNPQ.\)

\(\left\{ \begin{array}{l}
\left( \alpha \right) \cap \left( {ACD} \right) = PQ\\
AC//\left( \alpha \right)\\
AC \subset \left( {ACD} \right)
\end{array} \right. \Rightarrow PQ//AC\).

Mà \(MN//AC\) (câu a) nên \(MN//PQ.\)

Lại có: \(MQ//BD, NP//BD\) (câu a) nên \(MQ//NP.\)

Tứ giác \(MNPQ\) có hai cặp cạnh đối song song nên là hình bình hành.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 40 phiếu

Bài tiếp theo

Bài 3 trang 63 SGK Hình học lớp 11
Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi. Gọi O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp cắt bởi mặt phẳng (α) đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
Phương pháp tìm giao điểm của đường thẳng và mặt phẳng
Phương pháp tìm giao điểm của đường thẳng và mặt phẳng
Bài 1 trang 63 SGK Hình học lớp 11
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
Câu hỏi 2 trang 61 SGK Hình học 11
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. ...
Câu hỏi 1 trang 60 SGK Hình học 11
Trong phòng học hãy quan sát hình ảnh của đường thẳng song song với mặt phẳng....
Lý thuyết vị trí tương đối giữa đường thẳng và mặt phẳng
a và (P) có nhiều hơn một điểm chung: a ⊂ (P) (h.2.39a)
Lý thuyết Tính chất đường thẳng và mặt phẳng song song
Nếu đường thẳng a không nằm trên mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trên mặt phẳng (P) thì a song song với (P)