-
Toán 6 tập 1 - Chân trời sáng tạo
-
CHƯƠNG 1.SỐ TỰ NHIÊN
- Bài 1. Tập hợp. Phần tử của tập hợp
- Bài 2. Tập hợp số tự nhiên. Ghi số tự nhiên
- Bài 3. Các phép tính trong tập hợp số tự nhiên
- Bài 4. Lũy thừa với số mũ tự nhiên
- Bài 5. Thứ tự thực hiện các phép tính
- Bài 6. Chia hết và chia có dư. Tính chất chia hết của một tổng
- Bài 7. Dấu hiệu chia hết cho 2, cho 5
- Bài 8. Dấu hiệu chia hết cho 3, cho 9
- Bài 9. Ước và bội
- Bài 10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố
- Bài 11. Hoạt động thực hành và trải nghiệm
- Bài 12. Ước chung. Ước chung lớn nhất
- Bài 13. Bội chung. Bội chung nhỏ nhất
- Bài 14. Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 1
-
CHƯƠNG 2. SỐ NGUYÊN
-
-
Toán 6 tập 2 - Chân trời sáng tạo
-
GIẢI TOÁN 6 MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC XUẤT TẬP 1 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 SỐ VÀ ĐẠI SỐ TẬP 2 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 HÌNH HỌC VÀ ĐO LƯỜNG TẬP 2 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC XUẤT TẬP 2 CHÂN TRỜI SÁNG TẠO
Lý thuyết Các phép tính với số thập phân Toán 6 Chân trời sáng tạo
Tải vềLý thuyết Các phép tính với số thập phân Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
Tổng hợp đề thi học kì 1 lớp 6 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Khoa học tự nhiên...
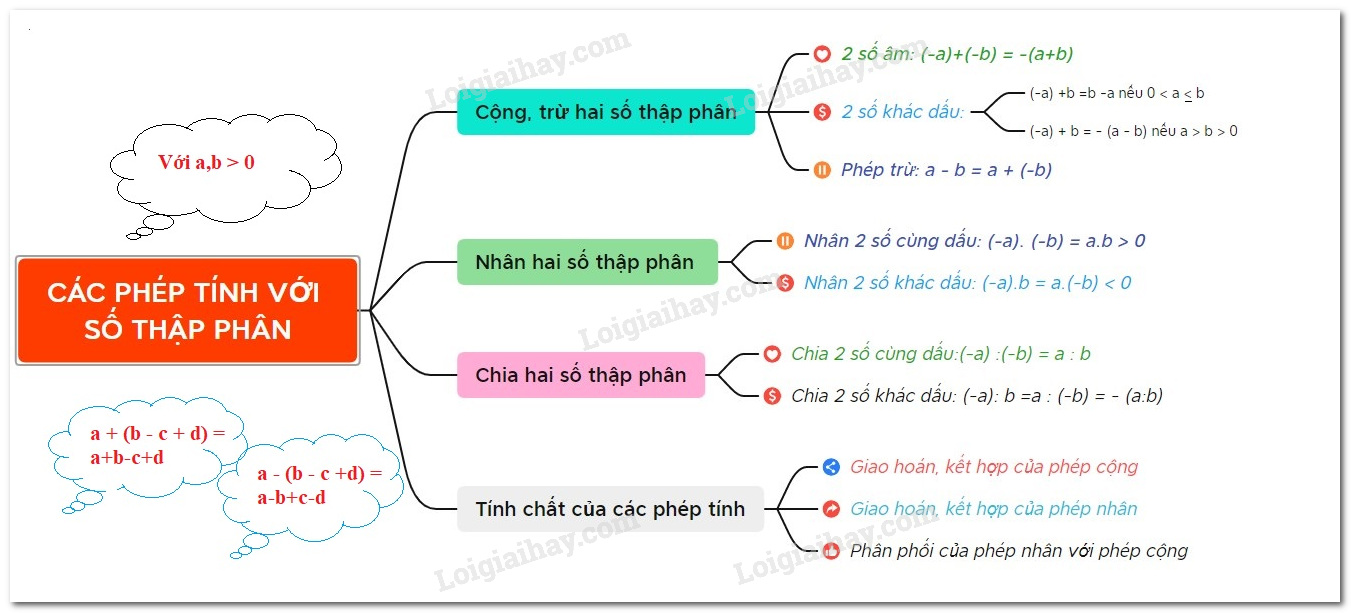
I. Cộng, trừ hai số thập phân
Cộng hai số thập phân âm:
$ \left( { - a} \right) + \left( { - b} \right) = - \left( {a + b} \right)$ với $ a,\,\,b > 0$
Cộng hai số thập phân khác dấu:
$ \left( { - a} \right) + b = b - a$ nếu $ 0 < a \le b$ ;
$ \left( { - a} \right) + b = - \left( {a - b} \right)$ nếu $ a > b > 0$ .
Phép trừ hai số thập phân được đưa về phép cộng với số đối:
$ a - b = a + \left( { - b} \right)$ .
Ví dụ:
a) $ \left( { - 24,5} \right) + \left( { - 3,16} \right) = - \left( {24,5 + 3,16} \right) = - 27,66$
b) $ 1,5 - 3,169 = 1,5 + \left( { - 3,169} \right) = - \left( {3,169 - 1,5} \right) = - 1,669;$
c) $ 25,689 - \left( { - 1,2345} \right) = 25,689 + 1,2345 = 26,9235$ .
II. Phép nhân hai số thập phân
Nhân hai số cùng dấu:
$ \left( { - a} \right).\left( { - b} \right) = a.b$ với $ a,\,\,b > 0$ .
Nhân hai số khác dấu:
$ \left( { - a} \right).b = a.\left( { - b} \right) = - \left( {a.b} \right)$ với $ a,\,b > 0$ .
Ví dụ:
a) Nhân hai số nguyên cùng dấu:
$ \left( { - 1,25} \right).\left( { - 2,41} \right) = 1,25.2,41 = 3,0125$ .
b) Nhân hai số nguyên khác dấu:
$ 2,72.\left( { - 3,25} \right) = - \left( {2,72.3,25} \right) = - 8,84$ .
III. Phép chia hai số thập phân
Chia hai số cùng dấu:
$ \left( { - a} \right):\left( { - b} \right) = a:b$ với $ a,\,\,b > 0$ .
Chia hai số khác dấu:
$ \left( { - a} \right):b = a:\left( { - b} \right) = - \left( {a:b} \right)$ với $ a,\,b > 0$ .
Ví dụ:
a) $ \left( {- 1,45} \right):\left( { - 2,5} \right) = 1,45:2,5 = 0,58$
b) $ \left( { - 5,24} \right):1,31 = - \left( {5,24:1,31} \right) = - 4$
IV. Tính chất của các phép tính với số thập phân
Giống như các phép tính với số nguyên và phân số, các phép tính với số thập phân cũng có đầy đủ các tính chất như:
- Tính chất giao hoán và tính chất kết hợp của phép cộng.
- Tính chất giao hoán và tính chất kết hợp của phép nhân.
- Tính chất phân phối của phép nhân đối với phép cộng.
V. Tính giá trị biểu thức chứa số thập phân
Vận dụng các tính chất của các phép tính với số thập phân và quy tắc dấu ngoặc, ta có thể tính giá trị các biểu thức một cách hợp lí.
Ví dụ:
$ \begin{array}{l}3,45 - 5,7 + 8,55 = \left( {3,45 + 8,55} \right) - 5,7\\ = 12 - 5,7 = 6,3\end{array}$
Bình luận
Chia sẻ
- Trả lời hoạt động khám phá 1 trang 32 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời thực hành 1 trang 33 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời vận dụng 1 trang 33 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời hoạt động khám phá 2 trang 33 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời thực hành 2 trang 34 SGK Toán 6 Chân trời sáng tạo Tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 6 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
