Bài 1.70 trang 45 SBT hình học 10

Giải bài 1.70 trang 45 sách bài tập hình học 10. Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD...

Đề bài

Cho hình chữ nhật \(ABCD\). Gọi \(I\) là giao điểm của hai đường chéo \(AC\) và \(BD\).

a) Với điểm \(M \) tùy ý, hãy chứng minh \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \);

b) Chứng minh rằng: \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\)

Phương pháp giải - Xem chi tiết

a) Sử dụng công thức trung điểm \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) với \(I\) là trung điểm của \(AB\).

b) Tính tổng hiệu các véc tơ và suy ra điều phải chứng minh.

Lời giải chi tiết

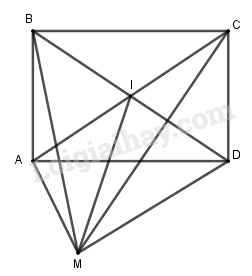
a) Ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MI} \); \(\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MI} \)

Vậy \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \).

b) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)\( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = AC\)

\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \)\( \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = DB\)

Vì hai đường chéo của hình chữ nhật dài bằng nhau nên \(AC = BD\) hay \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Bài 1.71 trang 46 SBT hình học 10
Giải bài 1.71 trang 46 sách bài tập hình học 10. Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI...
Bài 1.69 trang 45 SBT hình học 10
Giải bài 1.69 trang 45 sách bài tập hình học 10. Xét xem ba điểm sau có thẳng hàng không...
Bài 1.68 trang 45 SBT hình học 10
Giải bài 1.68 trang 45 sách bài tập hình học 10. Cho tứ giác ABCD.Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh rằng:...
Bài 1.67 trang 45 SBT hình học 10
Giải bài 1.67 trang 45 sách bài tập hình học 10. Cho ba lực...
Bài 1.66 trang 45 SBT hình học 10
Giải bài 1.66 trang 45 sách bài tập hình học 10. Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng:...
Bài 1.65 trang 45 SBT hình học 10
Giải bài 1.65 trang 45 sách bài tập hình học 10. Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA...
Bài 1.64 trang 45 SBT hình học 10
Giải bài 1.64 trang 45 sách bài tập hình học 10. Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác...
Bài 1.63 trang 44 SBT hình học 10
Giải bài 1.63 trang 44 sách bài tập hình học 10. Tìm tọa độ của vec tơ ...
Bài 1.62 trang 44 SBT hình học 10
Giải bài 1.62 trang 44 sách bài tập hình học 10. Cho a = (2; - 2) và b = (1;4)...
Bài 1.61 trang 44 SBT hình học 10
Giải bài 1.61 trang 44 sách bài tập hình học 10. Cho các điểm A'(-4;1), B'(2;4) và C'(2; - 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC...