-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 1.47 trang 42 SBT hình học 10
Giải bài 1.47 trang 42 sách bài tập hình học 10. Cho lục giác ABCDEF...
Đề bài
Cho lục giác đều \(ABCDEF\). Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó \(O\) là tâm của lục giác đều, hai véc tơ \(\overrightarrow i \) và \(\overrightarrow {OD} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {EC} \) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là \(6\).
Phương pháp giải - Xem chi tiết
Dựng hình, tính độ dài các đoạn thẳng và suy ra tọa độ cần tính.
Lời giải chi tiết
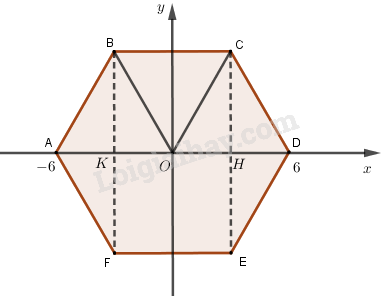
Từ hình vẽ ta thấy \(A\left( { - 6;0} \right)\) và \(D\left( {6;0} \right)\) (do các tam giác \(AOB\) và \(COD\) đều nên \(OA = OD = AB = 6\)).
Gọi \(H,K\) lần lượt là hình chiếu của \(C,B\) lên trục \(Ox\).
Khi đó \(CH = DC\sin {60^0} = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \)
\(OH = \sqrt {O{C^2} - C{H^2}} \) \(= \sqrt {{6^2} - {{\left( {3\sqrt 3 } \right)}^2}} = 3\)
Do đó \(C\left( {3;3\sqrt 3 } \right)\).
B đối xứng với C qua Oy nên B(-3; 3√3)
E đối xứng với C qua Ox nên E(3; -3√3)
F đối xứng với C qua O nên F(-3; -3√3))
Vậy \(A\left( { - 6;0} \right)\), \(D\left( {6;0} \right)\), \(B\left( { - 3;3\sqrt 3 } \right)\), \(C\left( {3;3\sqrt 3 } \right)\), \(E\left( {3; - 3\sqrt 3 } \right)\), \(F\left( { - 3; - 3\sqrt 3 } \right)\) .
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.46 trang 42 SBT hình học 10
- Bài 1.45 trang 42 SBT hình học 10
- Bài 1.44 trang 42 SBT hình học 10
- Bài 1.43 trang 42 SBT hình học 10
- Bài 1.42 trang 42 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
