-
ĐẠI SỐ SBT - TOÁN 10
-
HÌNH HỌC SBT - TOÁN 10
-
Chương 1: Véc tơ
-
Chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
- Bài 2: Tích vô hướng của hai vec tơ
- Bài 3: Các hệ thức lượng trong tam giác và giải tam giác
- Ôn tập chương 2: Tích vô hướng của hai véc tơ và ứng dụng
- Ôn tập chương 2: Đề toán tổng hợp
- Câu hỏi trắc nghiệm chương 2: Tích vô hướng của hai véc tơ và ứng dụng
-
Chương 3: Phương pháp tọa độ trong mặt phẳng
-
BÀI TẬP ÔN TẬP CUỐI NĂM
-
Bài 1.46 trang 42 SBT hình học 10
Giải bài 1.46 trang 42 sách bài tập hình học 10. Cho tam giác đều ABC cạnh a...
Đề bài
Cho tam giác đều \(ABC\) cạnh \(a\). Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó \(O \) là trung điểm của cạnh \(BC\), \(\overrightarrow i \) cùng hướng với \(\overrightarrow {OC} \), \(\overrightarrow j \) cùng hướng với \(\overrightarrow {OA} \).
a) Tính tọa độ của các đỉnh của tam giác \(ABC\).
b) Tìm tọa độ trung điểm \(E\) của \(AC\).
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác \(ABC\).
Phương pháp giải - Xem chi tiết
Dựng hình, tìm tọa độ các điểm dựa vào các tính chất hình học đã biết.
Lời giải chi tiết
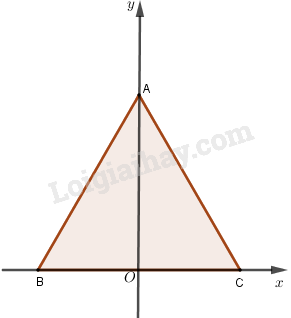
a) Do \(O\) là trung điểm \(CB\) nên \(OB = OC = \dfrac{a}{2}\) và \(OA = \sqrt {A{C^2} - O{C^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}\).
Từ hình vẽ ta suy ra \(A\left( {0;\dfrac{{a\sqrt 3 }}{2}} \right),B\left( { - \dfrac{a}{2};0} \right),C\left( {\dfrac{a}{2};0} \right)\)
b) Do \(E\) là trung điểm của \(AC\) nên \(\left\{ \begin{array}{l}{x_E} = \dfrac{{0 + \dfrac{a}{2}}}{2} = \dfrac{a}{4}\\{y_E} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0}}{2} = \dfrac{{a\sqrt 3 }}{4}\end{array} \right.\) nên \(E\left( {\dfrac{a}{4};\dfrac{{a\sqrt 3 }}{4}} \right)\)
c) Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm của tam giác.
Gọi \(G\) là trọng tâm tam giác thì \(\left\{ \begin{array}{l}{x_G} = \dfrac{{0 + \left( { - \dfrac{a}{2}} \right) + \dfrac{a}{2}}}{3} = 0\\{y_G} = \dfrac{{\dfrac{{a\sqrt 3 }}{2} + 0 + 0}}{3} = \dfrac{{a\sqrt 3 }}{6}\end{array} \right.\) hay \(G\left( {0;\dfrac{{a\sqrt 3 }}{6}} \right)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.47 trang 42 SBT hình học 10
- Bài 1.45 trang 42 SBT hình học 10
- Bài 1.44 trang 42 SBT hình học 10
- Bài 1.43 trang 42 SBT hình học 10
- Bài 1.42 trang 42 SBT hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
