Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đề số 1 – Đại số và giải tích 11

Đề bài

I. PHẦN TRẮC NGHIỆM

Câu 1: Với những giá trị nào của \(x\) thì giá trị của các hàm số tương ứng sau bằng nhau \(y = \tan 3x\) và \(\tan (\dfrac{\pi }{3} - 2x)\)

A. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\)

B.  \(x = \dfrac{\pi }{{15}} + k\pi ,\,k \in \mathbb{Z}\)

C. \(x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{2},\,k \in \mathbb{Z}\)

D. \(x = \dfrac{\pi }{5} + k\dfrac{\pi }{5},\,k \in \mathbb{Z}\)

Câu 2: Tìm m để phương trình \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m\) có nghiệm.

A. \( - 3 \le m \le 2\)              B. \(m > 2\)

C. \(m \ge  - 3\)                     D. \(\dfrac{2}{{11}} \le m \le 2\)

Câu 3: Nghiệm của phương trình  \(\sin x + \sqrt 3 \cos x = \sqrt 2 \) là:

A. \(x =  - \dfrac{\pi }{{12}} + k2\pi ,\;x = \dfrac{{5\pi }}{{12}} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

B. \(x =  - \dfrac{\pi }{4} + k2\pi ,\;x = \dfrac{{3\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

C. \(x = \dfrac{\pi }{3} + k2\pi ,\;x = \dfrac{{2\pi }}{3} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

D. \(x =  - \dfrac{\pi }{4} + k2\pi ,\;x =  - \dfrac{{5\pi }}{4} + k2\pi ,\;\left( {k \in \mathbb{Z}} \right).\)

Câu 4 : Chọn mệnh đề đúng:

A. Hàm số \(y = \sin x\) có chu kỳ \(T = \pi \)

B. Hàm số \(y = \cos x\) và hàm số \(y = \tan x\) có cùng chu kỳ.

C. Hàm số \(y = \cot x\) và hàm số \(y = \tan x\) có cùng chu kỳ.

D. Hàm số \(y = \cot x\) có chu kỳ \(T = 2\pi \)

Câu 5: Nghiệm dương bé nhất của phương trình \(2{\sin ^2}x + 5\sin x - 3 = 0\)  là:

A. \(x = \dfrac{\pi }{3}.\)     B. \(x = \dfrac{\pi }{{12}}.\)

C. \(x = \dfrac{\pi }{6}.\)     D. \(x = \dfrac{{5\pi }}{6}.\)

Câu 6: Hàm số nào sau đây có đồ thị không là đường hình sin?

A. \(y = \sin x\)                        B. \(y = \cos x\)

C. \(y = \sin 2x\)                      D. \(y = \cot x\)

Câu 7: Tập xác định của hàm số\(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1\) là:

A. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)   

B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)

C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}} \right\}\)     

D. \(\mathbb{R}\backslash \left\{ {\dfrac{{5\pi }}{{12}} + \dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\)

Câu 8: Nghiệm của phương trình \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3 \) là:

A. \(x = \dfrac{{5\pi }}{6} + k\pi \).                            

B. \(x = \dfrac{{5\pi }}{6} + k2\pi \).                          

C. \(x = \dfrac{\pi }{6} + k2\pi \).                               

D. \(x = \dfrac{\pi }{6} + k\pi \).

Câu 9: Tập nghiệm của phương trình \(\cos 3x =  - 1\) là:

A. \(\left\{ { - \dfrac{\pi }{2} + k2\pi |k \in \mathbb{Z}} \right\}.\) 

B. \(\left\{ {\pi  + k2\pi |k \in \mathbb{Z}} \right\}.\)

C. \(\left\{ {\dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\)       

D. \(\left\{ {\dfrac{{k2\pi }}{3}|k \in \mathbb{Z}} \right\}.\)

Câu 10: Trong các hàm số sau, hàm số nào là hàm số chẵn.

A. \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\).    

B. \(y = 2016\cos x + 2017\sin x\).

C. \(y = \cot 2015x - 2016\sin x\). 

D. \(y = \tan 2016x + \cot 2017x\).

Câu 11: Nghiệm của phương trình \(\sin 2x = \dfrac{{\sqrt 2 }}{2}\) là:

A.\(\,x = \dfrac{\pi }{8} + k2\pi ;x = \dfrac{{3\pi }}{8} + k2\pi (k \in Z)\)

B. \(\,x = \dfrac{\pi }{4} + k2\pi ;x = \dfrac{{3\pi }}{4} + k2\pi \,(k \in Z)\)

C.   \(\,x = \dfrac{\pi }{4} + k\pi ;x = \dfrac{{3\pi }}{4} + k\pi (k \in Z)\)

D. \(\,x = \dfrac{\pi }{8} + k\pi ;x = \dfrac{{3\pi }}{8} + k\pi ;k \in Z)\)

Câu 12: Giá trị nhỏ nhất m của hàm số \(y = 3\sin x + 1\) là.

A. m = 4                               B. m = -2 

C. m = 3                               D. m = 1

Câu 13: Tập xác định của hàm số \(y = f(x) = \dfrac{1}{{\sqrt {1 - sinx} }}\)

A. \(\mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)        

B. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)                 

C. \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}\)               

D. \(\phi \)

Câu 14: Giá trị nhỏ nhất của hàm số \(y = {\sin ^2}x - 4\sin x - 5\) là:

A. -9                                     B. 0

C. 9                                      D. -8

Câu 15: Đồ thị hàm số nào dưới đây nhận trục tung làm trục đối xứng?

A. \(y = \sin x - \cos x\).

B. \(y = 2\sin x\).

C. \(y = 2\sin \left( { - x} \right)\).

D. \(y =  - 2\cos x\)

Câu 16: Nghiệm của phương trình \(2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0\) là:

A. \(x = \dfrac{\pi }{4} + k\pi \); \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\)

B. \(x = \dfrac{\pi }{4} + k\pi ,k \in \mathbb{Z}\)

C. \(x = \dfrac{\pi }{4} + k\pi \);\(x = \arctan ( - 3) + k\pi ,k \in \mathbb{Z}\)

D. \(x = \arctan ( - \dfrac{3}{2}) + k\pi ,k \in \mathbb{Z}\)

Câu 17: Phương trình lượng giác nào dưới đây có nghiệm là: \(x = \dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\)

A. \(\cos 2x = \dfrac{{\sqrt 3 }}{2}.\)                          

B. \(\cot x = \sqrt 3 .\)    

C. \(\tan x = \sqrt 3 .\)     

D. \(\sin \left( {x - \dfrac{\pi }{3}} \right) =  - \dfrac{1}{2}\)

Câu 18: Giá trị lớn nhất M của hàm số \(y = \sin x + \cos x\) là.

A. \(M = 2\)                         

B. \(M = 2\sqrt 2 \)             

C. \(M = 1\)                         

D. \(M = \sqrt 2 \)

Câu 19: Nghiệm của phương trình \(\sin x = \cos x\) là:

A. \(x = \dfrac{\pi }{4} + k2\pi \).                               

B. \(x = \dfrac{\pi }{4} + k\pi \).                                 

C. \(x = \dfrac{\pi }{4}\).    

D. \(x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\).

Câu 20: Đồ thì hình bên là đồ thị của hàm số nào?

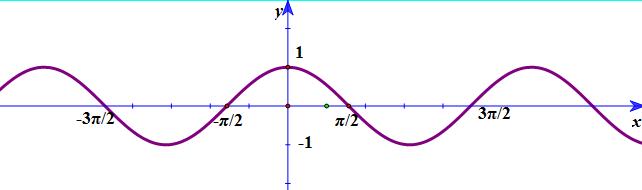
A. \(y = \sin x\)                     B. \(y = \cot x\)    

C. \(y = \tan x\)                    D. \(y = \cos x\)           

II. PHẦN TỰ LUẬN

Câu 21: Giải các phương trình sau

a) \(\sin 3x - \cos 2x = 0\)                                             

b) \(\dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0\)

Câu 22: Giải phương trình :   \(2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\)

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM

Câu 1:

Ta có: \(\tan 3x = \tan (\dfrac{\pi }{3} - 2x) \)\(\Leftrightarrow 3x = \dfrac{\pi }{3} - 2x + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow 5x = \dfrac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \dfrac{\pi }{{15}} + k\dfrac{\pi }{5}\;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án A.

Câu 2:

Ta có: \(\dfrac{{\cos x + 2\sin x + 3}}{{2\cos x - \sin x + 4}} = m \)

\(\Leftrightarrow \cos x + 2\sin x + 3 = m\left( {2\cos x - \sin x + 4} \right)\)

\( \Leftrightarrow \left( {2m - 1} \right)\cos x - \left( {m + 2} \right)\sin x = 3 - 4m\)

Điều kiện có nghiệm: \({\left( {2m - 1} \right)^2} + {\left( {m + 2} \right)^2} \ge {\left( {3 - 4m} \right)^2}\)

\( \Leftrightarrow 4{m^2} - 4m + 1 + {m^2} + 4m + 4\)\( \ge 9 - 24m + 16{m^2}\)

\( \Leftrightarrow 11{m^2} - 24m + 4 \le 0 \)\(\Leftrightarrow \dfrac{2}{{11}} \le m \le 2.\)

Chọn đáp án D.

Câu 3:

Ta có:\(\sin x + \sqrt 3 \cos x = \sqrt 2 \)

\(\begin{array}{l}
\Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = \frac{{\sqrt 2 }}{2}\\
\Leftrightarrow \cos \frac{\pi }{3}\sin x + \sin \frac{\pi }{3}\cos x = \frac{{\sqrt 2 }}{2}
\end{array}\)

\( \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 2 }}{2}\)

\( \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = \sin \dfrac{\pi }{4} \)\( \Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} = \pi  - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{12}} + k2\pi \\x = \dfrac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án A.

Câu 4:

+ Hàm số \(y = \sin x,\,y = \cos x\) có chu kỳ là \(T = 2\pi \)

+ Hàm số \(y = \tan x,y = \cot x\) có chu kì là \(T = \pi \)

Chọn đáp án C.

Câu 5:

Ta có: \(2{\sin ^2}x + 5\sin x - 3 = 0 \)\(\Leftrightarrow \left( {2\sin x - 1} \right)\left( {\sin x + 3} \right) = 0\)

\( \Leftrightarrow \sin x = \dfrac{1}{2} \)\(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

Nghiệm dương bé nhất của phương trình là \(x = \dfrac{\pi }{6}.\)

Chọn đáp án C.

Câu 6:

Hàm số \(y = \cot x\) có đồ thị không là đường hình sin.

Chọn đáp án D.

Câu 7:

\(y = f(x) = 2\cot (2x - \dfrac{\pi }{3}) + 1 \)\(= \dfrac{{2\cos (2x - \dfrac{\pi }{3})}}{{\sin (2x - \dfrac{\pi }{3})}} + 1\)

ĐKXĐ: \(\sin \left( {2x - \dfrac{\pi }{3}} \right) \ne 0 \)

\(\Leftrightarrow \left( {2x - \dfrac{\pi }{3}} \right) \ne k\pi \;\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x \ne \dfrac{\pi }{6} + k\dfrac{\pi }{2}\;\left( {k \in \mathbb{Z}} \right)\)
Chọn đáp án B.

Câu 8:

Ta có: \(\tan (x - \dfrac{\pi }{2}) = \sqrt 3  \)

\(\Leftrightarrow \tan (x - \dfrac{\pi }{2}) = \tan \dfrac{\pi }{3}\)

\( \Leftrightarrow x - \dfrac{\pi }{2} = \dfrac{\pi }{3} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \dfrac{{5\pi }}{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án A.

Câu 9:

Ta có: \(\cos 3x =  - 1 \Leftrightarrow 3x = \pi  + k2\pi \,\left( {k \in \mathbb{Z}} \right)\)

\( \Leftrightarrow x = \dfrac{\pi }{3} + k\dfrac{{2\pi }}{3}\;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án C.

Câu 10:

Đáp án A: TXĐ: D=R.

Ta có: 

\(\begin{array}{l}
y\left( { - x} \right) = \sin \left| { - 2016x} \right| + \cos \left( { - 2017x} \right)\\
= \sin 2016x + \cos 2017x = y\left( x \right)
\end{array}\)

Hàm số \(y = \sin \left| {2016x} \right| + c{\rm{os}}2017x\) là hàm số chẵn.

Chọn đáp án A.

Câu 11:

Ta có: \(\sin 2x = \dfrac{{\sqrt 2 }}{2} \Leftrightarrow \sin 2x = \sin \dfrac{\pi }{4}\)

\( \Leftrightarrow \left[ \begin{array}{l}2x = \dfrac{\pi }{4} + k2\pi \\2x = \pi  - \dfrac{\pi }{4} + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

\(\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + k\pi \\x = \dfrac{{3\pi }}{8} + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án D.

Câu 12:

Ta có: \(\sin x \in \left[ { - 1;1} \right] \)

\(\begin{array}{l}
\Rightarrow - 1 \le \sin x \le 1\\
\Rightarrow - 3 \le 3\sin x \le 3\\
\Rightarrow - 2 \le 3\sin x + 1 \le 4
\end{array}\)

Chọn đáp án B.

Câu 13:

Ta có: \(\sin x \in \left[ { - 1;1} \right] \Rightarrow 1 - \sin x \in \left[ {0;2} \right]\)

Điều kiện xác định: \(1 - \sin x \ne 0 \Leftrightarrow \sin x \ne 1 \)

\(\Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi  \;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án C.

Câu 14:

Ta có: \(y = {\sin ^2}x - 4\sin x - 5 \)\(= \left( {{{\sin }^2}x - 4\sin x + 4} \right) - 9 \)\(= {\left( {\sin x - 2} \right)^2} - 9\)

+ \(\sin x \in \left[ { - 1;1} \right] \Rightarrow \sin x - 2 \in \left[ { - 3; - 1} \right] \)

\(\Leftrightarrow {\left( {\sin x - 2} \right)^2} \in \left[ {1;9} \right]\)

Khi đó \(y \ge 1 - 9 =  - 8\)

Chọn đáp án D.

Câu 15:

Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng, do đó ta kiểm tra hàm số chẵn ở mỗi đáp án.

Dễ thấy hàm số \(y =  - 2\cos x\) là hàm chẵn nên nhận trục tung làm trục đối xứng.

Chọn đáp án D.

Câu 16:

Ta có: \(2{\sin ^2}x + \sin x\cos x - 3{\cos ^2}x = 0 \)

\(\Leftrightarrow \left( {\sin x - \cos x} \right)\left( {2\sin x + 3\cos x} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}\sin x = \cos x\\2\sin x =  - 3\cos x\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x =  - \dfrac{3}{2}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = \arctan \left( { - \dfrac{3}{2}} \right) + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án A.

Câu 17:

Ta có: \(\cot x = \sqrt 3  \Leftrightarrow x = \dfrac{\pi }{6} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án B.

Câu 18:

Ta có: \(y = \sin x + \cos x = \sqrt 2 \sin \left( {x + \dfrac{\pi }{4}} \right) \)

\(\begin{array}{l}
- 1 \le \sin \left( {x + \frac{\pi }{4}} \right) \le 1\\
\Rightarrow - \sqrt 2 \le \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) \le \sqrt 2
\end{array}\)

\(\Rightarrow y \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\)

Chọn đáp án D.

Câu 19:

Ta có: \(\sin x = \cos x \Leftrightarrow \tan x = 1 \)

\(\Leftrightarrow x = \dfrac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án B.

Câu 20:

Đồ thị hình bên là của hàm số \(y = \cos x\)

Chọn đáp án D.

II. PHẦN TỰ LUẬN

Câu 21:

\(a)  \sin 3x - \cos 2x = 0 \Leftrightarrow \sin 3x = \cos 2x \)\(\Leftrightarrow \sin 3x = \sin \left( {\dfrac{\pi }{2} - 2x} \right)\)

\(\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{l}
3x = \frac{\pi }{2} - 2x + k2\pi \\
3x = \pi - \frac{\pi }{2} + 2x + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
5x = \frac{\pi }{2} + k2\pi \\
x = \frac{\pi }{2} + k2\pi
\end{array} \right.
\end{array}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5}}\\{x = \dfrac{\pi }{2} + k2\pi }\end{array}} \right.\)

Vậy phương trình có nghiệm: \(x = \dfrac{\pi }{{10}} + k\dfrac{{2\pi }}{5};\,\,x = \dfrac{\pi }{2} + k2\pi \)\(\)

\(b) \dfrac{{\sin x + \sqrt 3 \cos x}}{{\sin x - \cos \dfrac{\pi }{4}}} = 0 \, (1)\)

ĐK: \(\sin x - \cos \dfrac{\pi }{4} \ne 0\)

\(\begin{array}{l}
\Leftrightarrow \sin x - \frac{{\sqrt 2 }}{2} \ne 0 \Leftrightarrow \sin x \ne \frac{{\sqrt 2 }}{2}\\
\Leftrightarrow \left\{ \begin{array}{l}
x \ne \frac{\pi }{4} + k2\pi \\
x \ne \frac{{3\pi }}{4} + k2\pi
\end{array} \right.\,\,\,\,\,\,\,\left( * \right)
\end{array}\)

\(\begin{array}{l}(1) \Leftrightarrow \sin x + \sqrt 3 \cos x = 0 \\\Leftrightarrow \dfrac{1}{2}\sin x + \dfrac{{\sqrt 3 }}{2}\cos x = 0 \\\Leftrightarrow \cos \dfrac{\pi }{3}\sin x + \sin \dfrac{\pi }{3}\cos x = 0\\ \Leftrightarrow \sin (x + \dfrac{\pi }{3}) = 0 \Leftrightarrow x + \frac{\pi }{3} = k\pi \\ \Leftrightarrow x = \dfrac{{ - \pi }}{3} + k\pi \end{array}\)

Kết hợp với điều kiện (*) ta thấy thỏa mãn.

Vậy phương trình có nghiệm: \(x = \dfrac{{ - \pi }}{3} + k\pi \)

Câu 22:

\(2{\cos ^2}\left( {\dfrac{\pi }{4} - 2x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\)

\( \Leftrightarrow 1 + \cos \left( {\dfrac{\pi }{2} - 4x} \right) + \sqrt 3 \cos 4x = 4{\cos ^2}x - 1\)\(\Leftrightarrow \sin 4x + \sqrt 3 \cos 4x = 2\left( {2{{\cos }^2}x - 1} \right)\)

\(\begin{array}{l} \Leftrightarrow \dfrac{1}{2}\sin 4x + \dfrac{{\sqrt 3 }}{2}\cos 4x = \cos 2x \\\Leftrightarrow \sin \dfrac{\pi }{6}\sin 4x + \cos \dfrac{\pi }{6}\cos 4x = \cos 2x\\ \Leftrightarrow \cos \left( {4x - \dfrac{\pi }{6}} \right) = \cos 2x \end{array}\)

\(\begin{array}{l}
\Leftrightarrow \left[ \begin{array}{l}
4x - \frac{\pi }{6} = 2x + k2\pi \\
4x - \frac{\pi }{6} = - 2x + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
2x = \frac{\pi }{6} + k2\pi \\
6x = \frac{\pi }{6} + k2\pi
\end{array} \right.
\end{array}\)

\(\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{\pi }{{12}} + k\pi }\\{x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}}\end{array}} \right.\,\,(k \in \mathbb{Z})\)

Vậy phương trình có nghiệm là: \(x = \dfrac{\pi }{{12}} + k\pi ;\,x = \dfrac{\pi }{{36}} + k\dfrac{\pi }{3}\)

Loigiaihay.com