 Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
Giải toán 11, giải bài tập toán lớp 11 đầy đủ đại số và giải tích, hình học
 Đề kiểm tra 15 phút – Chương 2 – Đại số và giải tích 11
Đề kiểm tra 15 phút – Chương 2 – Đại số và giải tích 11
Đề kiểm tra 15 phút – Chương 2 – Đề số 5 – Đại số và giải tích 11
Đáp án và lời giải chi tiết Đề thi kiểm tra 15 phút – Chương 2 – Đề số 5 – Đại số và giải tích 11
Đề bài
Câu 1: Một thí sinh phải chọn 10 trong số 20 câu hỏi. Hỏi có bao nhiêu cách chọn 10 câu hỏi này nếu 3 câu đầu phải được chọn:
A. \(C_{20}^{10}\) B. \(C_7^{10} + C_{10}^3\)
C. \(C_{10}^7.C_{10}^3\) D. \(C_{17}^7\)
Câu 2: Giá trị của \(n \in \mathbb{N}\) thỏa mãn đẳng thức \(C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 = 2C_{n + 2}^8\) là:
A. n = 18 B. n = 16
C. n = 15 D. n = 14
Câu 3: Trong các câu sau, câu nào sai:
A. \(C_{14}^3 = C_{14}^{11}\)
B. \(C_{10}^3 + C_{10}^4 = C_{11}^4\)
C. \(C_4^0 + C_4^1 + C_4^2 + C_4^3 + C_4^4 = 16\)
D. \(C_{10}^4 + C_{11}^4 = C_{11}^5\)
Câu 4: Nếu \(A_x^2 = 110\) thì
A. x =10
B. x = 11
C. x = 11 hay x = 10
D. x = 0
Câu 5: Trong mặt phẳng cho 2010 điểm phân biệt sao cho 3 điểm bất kỳ không thẳng hàng. Hỏi có bao nhiêu véc tơ khác véc tơ – không có điểm đầu và điểm cuối thuộc 2010 điểm đã cho.
A. 4039127 B. 4038090
C. 4167114 D. 167541284
Câu 6: Cho biết \(C_n^{n - k} = 28\). Giá trị của n và k lần lượt là:
A. 8 và 4
B. 8 và 3
C. 8 và 2
D. Không thể tìm được
Câu 7: Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:
A. 11 B. 10
C. 9 D. 8
Câu 8: Nghiệm của phương trình \(A_n^3 = 20n\) là :
A. n = 6 B. n = 5
C. n = 8 D. Không tồn tại
Câu 9: Cho đa giác đều n đỉnh, \(n \in \mathbb{N}\)và \(n \ge 3\). Tìm n biết rằng đa giác đã cho có 135 đường chéo
A. n = 15 B. n = 27
C. n = 8 D. n = 18
Câu 10: Giải bất phương trình ( ẩn n thuộc tập tự nhiên ) \(\dfrac{{C_{n + 1}^2}}{{C_n^2}} \ge \dfrac{3}{{10}}n\)
A. \(2 \le n < 4\)
B. \(0 \le n \le 2\)
C. \(1 \le n \le 5\)
D. \( - {2 \over 3} \le n \le 5\)
Lời giải chi tiết
|
1D |
2C |
3D |
4B |
5B |
|
6C |
7A |
8A |
9D |
10D |
Câu 1:
Theo yêu cầu bài toán:
+ 3 câu đầu phải được chọn thì chỉ có 1 cách
+ Chọn 7 câu trong 17 câu còn lại có: \(C_{17}^7\) cách
Vậy có \(C_{17}^7\) cách.
Chọn đáp án D.
Câu 2:
Điều kiện: \(n \ge 9\)
Ta có: \(C_n^6 + 3C_n^7 + 3C_n^8 + C_n^9 = 2C_{n + 2}^8\)
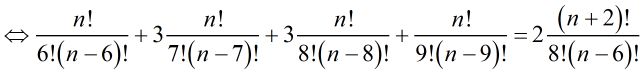
Giải phương trình này có: \(n = 15\)
Chọn đáp án C.
Câu 3:
Ta có: \(\left\{ \begin{array}{l}C_{10}^4 + C_{11}^4 = 540\\C_{11}^5 = 462\end{array} \right.\)\(\, \Rightarrow C_{10}^4 + C_{11}^4 \ne C_{11}^5 = 462\)
Chọn đáp án D.
Câu 4:
Điều kiện: \(x \ge 2\)
Ta có: \(A_x^2 = 110 \Leftrightarrow \dfrac{{x!}}{{\left( {x - 2} \right)!}} = 110\)
\( \Leftrightarrow x\left( {x - 1} \right) = 110 \Rightarrow x = 11\)
Chọn B
Câu 5:
Số véc tơ khác véc tơ không có điểm đầu và điểm cuối thuộc 2010 điểm đã cho là \(C_{2010}^2 = 4038090\) (cách)
Chọn đáp án B.
Câu 6:
Ta có: \(C_n^{n - k} = 28 \Leftrightarrow \dfrac{{n!}}{{\left( {n - k} \right)!k!}} = 28\)\( \Leftrightarrow \left\{ \begin{array}{l}n = 8\\k = 2\end{array} \right.\)
Chọn đáp án C.
Câu 7:
Số đường chéo của đa giác được xác định bởi công thức
\(\dfrac{{n\left( {n - 3} \right)}}{2} = 44 \)
\(\Leftrightarrow {n^2} - 3n - 88 = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}n = 11\\n = - 8\end{array} \right.\)
Chọn đáp án A.
Câu 8:
Điều kiện: \(n \ge 3\)
Ta có: \(A_n^3 = 20n \Leftrightarrow \dfrac{{n!}}{{\left( {n - 3} \right)!}} = 20n\)
\(\Leftrightarrow n\left( {n - 1} \right)\left( {n - 2} \right) = 20n\)
\( \Leftrightarrow \left( {n - 1} \right)\left( {n - 2} \right) = 20 \Leftrightarrow \left[ \begin{array}{l}n = 6\\n = - 3\end{array} \right.\)
Chọn đáp án A.
Câu 9:
Số đường chéo của đa giác được xác định bằng công thức:
\(\dfrac{{n\left( {n - 3} \right)}}{2} = 135\)
\(\Leftrightarrow {n^2} - 3n - 270 = 0 \)
\(\Leftrightarrow \left[ \begin{array}{l}n = 18\\n = - 15\end{array} \right.\)
Chọn đáp án D.
Câu 10:
Điều kiện: \(n \ge 2\)
Ta có: \(\dfrac{{C_{n + 1}^2}}{{C_n^2}} \ge \dfrac{3}{{10}}n\)
\(\Leftrightarrow \dfrac{{\dfrac{{\left( {n + 1} \right)!}}{{2!\left( {n - 1} \right)!}}}}{{\dfrac{{n!}}{{2!\left( {n - 2} \right)!}}}} \ge \dfrac{3}{{10}}n \)
\(\Leftrightarrow \dfrac{{n\left( {n + 1} \right)}}{{n\left( {n - 1} \right)}} \ge \dfrac{3}{{10}}n\)
\( \Leftrightarrow \dfrac{{n + 1}}{{n - 1}} \ge \dfrac{3}{{10}}n \)
\(\Leftrightarrow 10n + 10 \ge 3{n^2} - 3n\)
\( \Leftrightarrow 3{n^2} - 13n - 10 \le 0\)
\(\Leftrightarrow - \dfrac{2}{3} \le n \le 5\)
Chọn đáp án D
Loigiaihay.com
- Đề kiểm tra 15 phút – Chương 2 – Đề số 6 – Đại số và giải tích 11
- Đề kiểm tra 15 phút – Chương 2 – Đề số 7 – Đại số và giải tích 11
- Đề kiểm tra 15 phút – Chương 2 – Đề số 8 – Đại số và giải tích 11
- Đề kiểm tra 15 phút – Chương 2 – Đề số 9 – Đại số và giải tích 11
- Đề kiểm tra 15 phút – Chương 2 – Đề số 4 – Đại số và giải tích 11
>> Xem thêm












Danh sách bình luận