Câu hỏi 2 trang 93 SGK Đại số và Giải tích 11

Cho (u_n) là một cấp số cộng có sáu số hạng với ...

Đề bài

Cho \((u_n)\) là một cấp số cộng có sáu số hạng với \(\displaystyle u_1 ={{ - 1} \over 3},d = 3\). Viết dạng khai triển của nó.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Tính từ số hạng của CSC và kết luận.

Sử dụng công thức \({u_{n + 1}} = {u_n} + d\)

Lời giải chi tiết

Ta có:

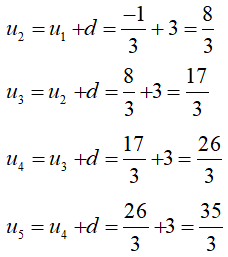
\({u_6} = u_5 + d ={u_5} + 3\) \( = \frac{{35}}{3} + 3 = \frac{{44}}{3}\)

Dạng khai triển của cấp số cộng đó là: \(\displaystyle{{ - 1} \over 3};\,{8 \over 3};\,{{17} \over 3};\,{{26} \over 3};\,{{35} \over 3};\frac{{44}}{3} \)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 13 phiếu

Bài tiếp theo

Câu hỏi 3 trang 94 SGK Đại số và Giải tích 11
Mai và Hùng chơi trò xếp các que diêm thành hình tháp trên mặt sân. Cách xếp được thể hiện trên Hình 42.
Câu hỏi 4 trang 96 SGK Đại số và Giải tích 11
Cấp số cộng gồm tám số hạng -1, 3, 7, 11, 15, 19, 23, 27 được viết vào bảng sau...
Bài 1 trang 97 SGK Đại số và Giải tích 11
Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tính số hạng đầu và công sai của nó:
Bài 2 trang 97 SGK Đại số và Giải tích 11
Tìm số hạng đầu và công sai của các cấp số cộng sau, biết:
Bài 3 trang 97 SGK Đại số và Giải tích 11
Trong các bài toán về cấp số cộng, ta thường gặp năm đại lượng
Bài 4 trang 98 SGK Đại số và Giải tích 11
Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân 0,5 m. Cầu thang đi từ tầng một lên tầng 2 gồm 21 bậc, mỗi bậc cao 18 cm.
Bài 5 trang 98 SGK Đại số và Giải tích 11
Từ giờ đến 12 giờ trưa, đồng hồ đánh bao nhiêu tiếng, nếu nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ
Câu hỏi 1 trang 93 SGK Đại số và Giải tích 11
Giải câu hỏi 1 trang 93 SGK Đại số và Giải tích 11. Biết bốn số hạng đầu của một dãy số là -1, 3, 7, 11....
Lý thuyết cấp số cộng