Câu hỏi 2 trang 13 SGK Hình học 11

Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo...

Đề bài

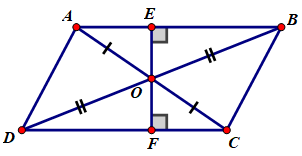
Cho hình bình hành \(ABCD\). Gọi \(O\) là giao điểm của hai đường chéo. Đường thẳng kẻ qua \(O\) vuông góc với \(AB,\) cắt \(AB\) ở \(E\) và cắt \(CD\) ở \(F.\) Hãy chỉ ra các cặp điểm trên hình vẽ đối xứng với nhau qua tâm \(O\).

Video hướng dẫn giải

Lời giải chi tiết

- Hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo \(⇒ O\) là trung điểm mỗi đường nên \(A\) và \(C\) đối xứng nhau qua tâm \(O\).

\(B\) và \(D\) đối xứng nhau qua tâm \(O\)

- Xét hai tam giác vuông \(AEO\) và \(CFO\) có:

\(OA = OC\) (do \(O\) là trung điểm \(AC\))

\(∠(AOE) = ∠(COF)\) (hai góc đối đỉnh)

\(⇒ ΔAEO = ΔCFO\) (cạnh huyền – góc nhọn kề)

\(⇒ OE = OF \)(hai cạnh tương ứng)

Nên \(O\) là trung điểm \(EF\)

\(⇒ E\) và \(F\) đối xứng nhau qua tâm \(O\).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 9 phiếu

Bài tiếp theo

Câu hỏi 3 trang 13 SGK Hình học 11
Trong mặt phẳng tọa độ Oxy cho điểm A(- 4; 3). Tìm ảnh của A qua phép đối xứng tâm O....
Câu hỏi 4 trang 14 SGK Hình học 11
Chọn hệ tọa độ Oxy...
Câu hỏi 5 trang 15 SGK Hình học 11
Giải câu hỏi 5 trang 15 SGK Hình học 11. Trong các chữ sau, chữ nào là hình có tâm đối xứng?...
Câu hỏi 6 trang 15 SGK Hình học 11
Giải câu hỏi 6 trang 15 SGK Hình học 11. Tìm một số hình tứ giác có tâm đối xứng...
Bài 1 trang 15 SGK Hình học 11
Trong mặt phẳng tọa độ Oxy cho điểm A(-1;3) và đường thẳng d có phương trình x-2y + 3 = 0. Tìm ảnh của A và d qua phép đối xứng tâm O.
Bài 2 trang 15 SGK Hình học 11
Trong các hình tam giác đều, hình bình hành, ngũ giác đều, lục giác đều, hình nào có tâm đối xứng?
Bài 3 trang 15 SGK Hình học 11
Tìm một hình có vô số tâm đối xứng?
Câu hỏi 1 trang 13 SGK Hình học 11
Chứng minh rằng...
Lý thuyết phép đối xứng tâm
Cho điểm O/ Phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành M' sao cho O là trung điểm của đoạn thẳng MM' được gọi là phép đối xứng tâm O.