Giải SBT toán hình học và giải tích 12 nâng cao Bài 1: Mặt cầu, khối cầu

Bài 17 trang 56 SBT Hình học 12 Nâng cao


Giải bài 17 trang 56 sách bài tập Hình học 12 Nâng cao. Trong số các hình chóp tam giác đều ngoại tiếp

Đề bài

Trong số các hình chóp tam giác đều ngoại tiếp một mặt cầu bán kính r cho trước, tìm hình chóp có diện tích toàn phần nhỏ nhất.

Lời giải chi tiết

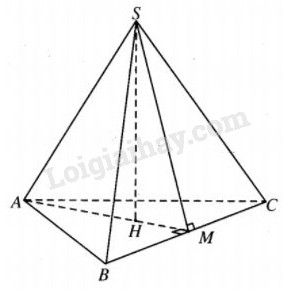
Kí hiệu cạnh đáy của hình chóp là a, chiều cao là h, thể tích khối chóp là V, diện tích toàn phần là Stp thì \(r = {{3V} \over {{S_{tp}}}}\), tức là \({S_{tp}} = {{3V} \over r}\). Vậy Stp nhỏ nhất khi và chỉ khi V nhỏ nhất.

Mặt khác, cũng từ hệ thức \({S_{tp}} = {{3V} \over r}\), ta có hệ thức liên hệ giữa a, h và r là

\(\eqalign{  & r = {{ah} \over {a + \sqrt {{a^2} + 12{h^2}} }}\;\;\;\;(1)  \cr  & \left( {V = {1 \over 3}.{{{a^2}\sqrt 3 } \over 4}.h = {{\sqrt 3 } \over {12}}{a^2}.h} \right). \cr} \)

Gọi M là trung diểm của BC và đặt \(\widehat {SMH}\) =\(\varphi \)  (đó là góc giữa mp(SBC) và mp(ABC), cũng là góc giữa mặt bên và mặt đáy của hình chóp). Khi ấy

\(h = {{a\sqrt 3 } \over 6}\tan \varphi \;\;\;\;(2)\)

Thay (2) vào (1), ta có \(a = {{6r(\cos \varphi  + 1)} \over {\sqrt 3 \sin \varphi }},\) từ đó thay vào (2), ta có \(h = {{r(\cos \varphi  + 1)} \over {\cos \varphi }}\)

Suy ra \({a^2} = 12{r^2}{{1 + \cos \varphi } \over {1 - \cos \varphi }},\)

Vậy

 \(\eqalign{   V& = {{\sqrt 3 } \over {12}}.12{r^2}.{{1 + \cos \varphi } \over {1 - \cos \varphi }}.r.{{1 + \cos \varphi } \over {\cos \varphi }}  \cr  &  = \sqrt 3 .{r^3}{{{{(1 + \cos \varphi )}^2}} \over {{\rm{cos}}\varphi {\rm{(1 - cos}}\varphi {\rm{)}}}} = \sqrt 3 .{r^3}{{{{(1 + t)}^2}} \over {t(1 - t)}} \cr} \)

với \(0<t=cos\varphi  <1\).

Xét hàm số \(f(t) = {{{{(1 + t)}^2}} \over {t(1 - t)}},0 < t < 1,\) thì V nhỏ nhất khi và chỉ khi f(t) nhỏ nhất.

Ta có:

\(\eqalign{
 f'(t) &= {{2\left( {1 + t} \right)t\left( {1 - t} \right) - {{\left( {1 + t} \right)}^2}\left( {1 - 2t} \right)} \over {{t^2}{{\left( {1 - t} \right)}^2}}} \cr 
& = {{2\left( {t - {t^3}} \right) - \left( {1 - 3{t^2} - 2{t^3}} \right)} \over {{t^2}{{\left( {1 - t} \right)}^2}}} \cr 
& = {{3{t^2} + 2t - 1} \over {{t^2}{{\left( {1 - t} \right)}^2}}} \cr} \)

\(f'(t) = 0 \Leftrightarrow t = {1 \over 3}.\)

Xét bảng biến thiên sau

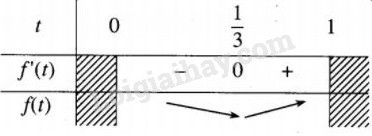
Vậy f(t) đạt giá trị nhỏ nhất khi và chỉ khi \(t = {1 \over 3}\), tức là \(\cos \varphi  = {1 \over 3}.\)

Khi đó h=4r, \(\tan \varphi  = 2\sqrt 2 ,\) từ đó \(a = 2r\sqrt 6 .\)

Vậy khi \(a = 2r\sqrt 6 \), \(h=4r\) thì diện tích toàn phần của hình chóp đạt giá trị nhỏ nhất.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store