-
Toán 6 tập 1 - Chân trời sáng tạo
-
CHƯƠNG 1.SỐ TỰ NHIÊN
- Bài 1. Tập hợp. Phần tử của tập hợp
- Bài 2. Tập hợp số tự nhiên. Ghi số tự nhiên
- Bài 3. Các phép tính trong tập hợp số tự nhiên
- Bài 4. Lũy thừa với số mũ tự nhiên
- Bài 5. Thứ tự thực hiện các phép tính
- Bài 6. Chia hết và chia có dư. Tính chất chia hết của một tổng
- Bài 7. Dấu hiệu chia hết cho 2, cho 5
- Bài 8. Dấu hiệu chia hết cho 3, cho 9
- Bài 9. Ước và bội
- Bài 10. Số nguyên tố. Hợp số. Phân tích một số ra thừa số nguyên tố
- Bài 11. Hoạt động thực hành và trải nghiệm
- Bài 12. Ước chung. Ước chung lớn nhất
- Bài 13. Bội chung. Bội chung nhỏ nhất
- Bài 14. Hoạt động thực hành và trải nghiệm
- Bài tập cuối chương 1
-
CHƯƠNG 2. SỐ NGUYÊN
-
-
Toán 6 tập 2 - Chân trời sáng tạo
-
GIẢI TOÁN 6 MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC XUẤT TẬP 1 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 SỐ VÀ ĐẠI SỐ TẬP 2 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 HÌNH HỌC VÀ ĐO LƯỜNG TẬP 2 CHÂN TRỜI SÁNG TẠO
-
GIẢI TOÁN 6 MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC XUẤT TẬP 2 CHÂN TRỜI SÁNG TẠO
Lý thuyết Số thập phân Toán 6 Chân trời sáng tạo
Tải vềLý thuyết Số thập phân Toán 6 Chân trời sáng tạo ngắn gọn ,đầy đủ, dễ hiểu
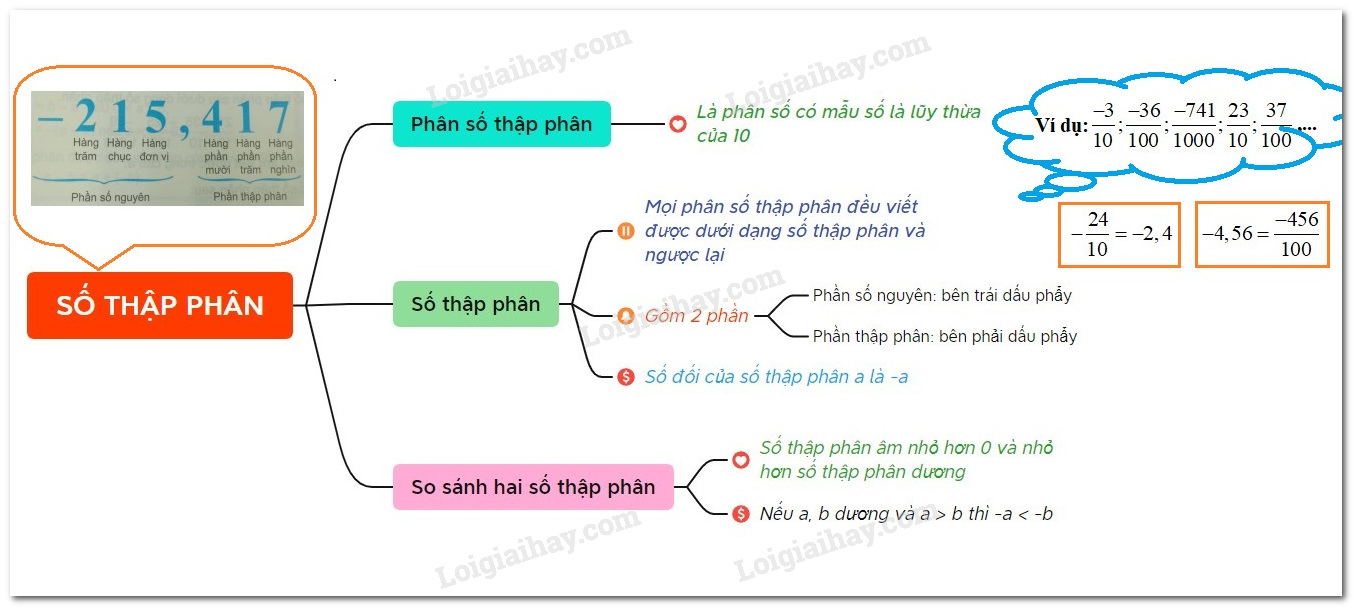
I. Phân số thập phân và số thập phân âm
Phân số thập phân là là phân số mà mẫu là lũy thừa của $10$.
Ví dụ:
$\dfrac{7}{{10}};\dfrac{{ - 15}}{{1000}};...$ là các phân số thập phân.
- Ta viết $ - \dfrac{{15}}{{10}} = - 1,5$ và gọi $ - 1,5$ là số thập phân âm, đọc là “ âm một phẩy năm”.
- Các số $2,3;\,\,0,24;...$gọi là các số thập phân dương, đôi khi còn được viết là $ + 2,3;\,\, + 0,24;...$
- Các số thập phân dương và các số thập phân âm gọi chung là số thập phân.
Nhận xét:
- Mọi phân số thập phân đều viết được dưới dạng số thập và ngược lại.
- Số thập phân gồm hai phần:
+ Phần số nguyên viết bên trái dấu phẩy;
+ Phần thập phân viết bên phải dấu phẩy.
II. So sánh hai số thập phân
- Số thập phân âm nhỏ hơn $0$ và nhỏ hơn số thập phân dương
- Nếu $a,b$ là hai số thập phân dương và $a > b$ thì $ - a < - b$.
Ví dụ:
a) $2,34 < 5,21$
b) Do $2,3 > 1,5$ nên $ - 2,3 < - 1,5$.
Chú ý:
Nếu $a < b$ và $b < c$ thì $a < c$.
III. Số đối của một số thập phân
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ:
Số đối của $ - 1,5$ là $1,5$.
Số đối của $24,3$ là $ - 24,3$
Bình luận
Chia sẻ
- Trả lời hoạt động khám phá 1 trang 29 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời thực hành 1 trang 30 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời hoạt động khám phá 2 trang 30 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời thực hành 2 trang 30 SGK Toán 6 Chân trời sáng tạo Tập 2
- Trả lời hoạt động khám phá 3 trang 30 SGK Toán 6 Chân trời sáng tạo Tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 6 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
