Bài tập trắc nghiệm trang 186, 187 SBT Đại số 10

6.24

Cho cotα = -2/3 với π < α < π. Giá trị cosα là

A. \( - \dfrac{2}{{\sqrt {13} }}\)

B. \(\dfrac{2}{{\sqrt {13} }}\)

C. \(\dfrac{2}{5}\)

D. \( - \dfrac{{\sqrt {13} }}{2}\)

Lời giải chi tiết:

Cách 1.

1/( sin² α) = 1 + cot² α = 1 + 4/9 = 13/9 ⇒ sin² α = 9/13.

Suy ra sinα = ±3/√13.

Vì π/2 < α < π nên sinα > 0. Vậy sinα = 3/√13.

Từ đó cosα = sinα.cotα = (-2)/√13.

Đáp án là A.

Cách 2.

cotα = (-2)/3 ⇒ tanα = (-3)/2;

1/( cos² α) = 1 + tan² α = 1 + 9/4 = 13/4 ⇒ cos² α = 4/13.

Suy ra cosα = ±2/√13. Vì π/2 < α < π nên cosα < 0.

Vậy cosα = (-2)/√13 và đáp án là A.

Đáp án: A

6.25

Cho tanα = -√2/3. Giá trị của biểu thức \(M = \dfrac{{3\cos \alpha  - 5\sin \alpha }}{{ - 2\cos \alpha  + 3\sin \alpha }}\) là

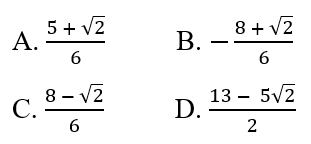
Lời giải chi tiết:

Cách 1. Suy luận

Vì tanα < 0 nên cosα và sinα trái dấu.

Nếu cosα > 0, sinα < 0 thì tử số của M dương, còn mẫu số âm, nên M < 0. Còn nếu cosα < 0, sinα > 0 thì tử số của M âm, mẫu số của M dương nên ta cũng có M < 0.

Do đó các phương án A, C, D bị loại và đáp án là B.

Cách 2. Tính trực tiếp.

Chia cả tử và mẫu của M sao cho cosα, ta được:

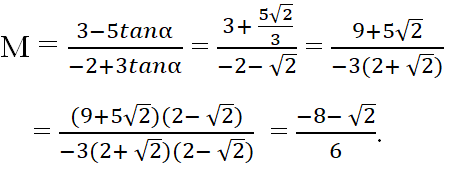
Đáp án: B

6.26

Cho cosα = √2/3 (0 <α < π/2 ). Giá trị của cot(α + 3π/2) là

Lời giải chi tiết:

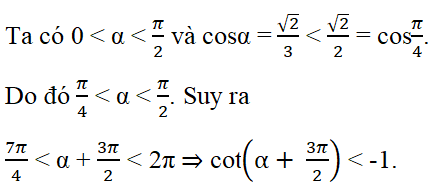
Vậy các phương án B, C, D bị loại và đáp án là A.

Đáp án: A

Cách khác:

Ta có: \(\cos \alpha  = \dfrac{{\sqrt 2 }}{3}\) \( \Rightarrow {\sin ^2}\alpha  = 1 - {\cos ^2}\alpha \) \( = 1 - \dfrac{2}{9} = \dfrac{7}{9}\)

\( \Rightarrow \sin \alpha  =  \pm \dfrac{{\sqrt 7 }}{3}\)

Vì \(0 < \alpha  < \dfrac{\pi }{2}\) nên \(\sin \alpha  > 0\), do đó \(\sin \alpha  = \dfrac{{\sqrt 7 }}{3}\)

\( \Rightarrow \tan \alpha  = \dfrac{{\sin \alpha }}{{\cos \alpha }}\) \( = \dfrac{{\sqrt 7 }}{3}:\dfrac{{\sqrt 2 }}{3} = \dfrac{{\sqrt {14} }}{2}\)

Mà \(\cot \left( {\alpha  + \dfrac{{3\pi }}{2}} \right)\)\( = \cot \left( {2\pi  - \dfrac{\pi }{2} + \alpha } \right)\) \( = \cot \left( { - \dfrac{\pi }{2} + \alpha } \right)\)

 \( = \cot \left[ { - \left( {\dfrac{\pi }{2} - \alpha } \right)} \right]\) \( =  - \cot \left( {\dfrac{\pi }{2} - \alpha } \right)\) \( =  - \tan \alpha  =  - \dfrac{{\sqrt {14} }}{2}\)

Vậy \(\cot \left( {\alpha  + \dfrac{{3\pi }}{2}} \right) =  - \dfrac{{\sqrt {14} }}{2}\).

6.27

Cho tanα + cotα = -2. Giá trị của biểu thức N = tan³α + cot³α là

    A. 3            B. 4

    C. -2            D. 2

Lời giải chi tiết:

Cách 1.

Ta có:

\(\begin{array}{l}{\left( {\tan \alpha  + \cot \alpha } \right)^2}\\ = {\tan ^2}\alpha  + {\cot ^2}\alpha  + 2\tan \alpha \cot \alpha \\ = \left( {{{\tan }^2}\alpha  + {{\cot }^2}\alpha } \right) + 2\\ \ge 2\tan \alpha \cot \alpha  + 2 = 2.1 + 2 = 4\\ \Rightarrow {\left( {\tan \alpha  + \cot \alpha } \right)^2} \ge 4\\ \Rightarrow \left[ \begin{array}{l}\tan \alpha  + \cot \alpha  \ge 2\\\tan \alpha  + \cot \alpha  \le  - 2\end{array} \right.\end{array}\)

Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.

Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.

Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.

Do đó tan³ α + cot³ α = -2

Đáp án là C.

Cách 2.

Áp dụng công thức

tan³ α + cot³ α = (tanα + cotα)( tan² α – tanα.cotα + cot² α)

= -2( tan² α + cot² α – 1)

Mà tan² α + cot² α = (tanα + cotα)² - 2 tanα.cotα = 4 – 2 = 2.

Vậy tan³ α + cot³ α = -2(2-1) = -2.

Đáp án: C

6.28

Cho sinα = √5/4. Giá trị cos(α + π/2) là

A. \( - \dfrac{{4\sqrt 5 }}{5}\)                    B. \(\dfrac{{\sqrt 5 }}{4}\)

C. \(\dfrac{{\sqrt 3 }}{4}\)              D. \( - \dfrac{{\sqrt 5 }}{4}\)

Lời giải chi tiết:

Cách 1

Ta có sinα > 0 nên

k2π < α < π + k2π, k ∈ Z ⇒ π/2 + k2π < α + π/2 < 3π/2 + k2π.

Do đó cos(α+ π/2) < 0, nên các phương án B, C bị loại. Mặt khác cos(α+ π/2) > -1 nên phương án A bị loại. Vậy đáp án là D.

Cách 2. Ta có

cos(α+ π/2) = cos(α- π/2+ π) = - cos(α- π/2) = - cos(π/2- α) = - sin α = -√5/4

Đáp án: D 

6.29

Cho sinα = √6/3. Giá trị của biểu thức

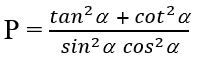
A. 51/7            B. 31/4

C. 45/4            D. 22/3

Lời giải chi tiết:

Cách 1. Suy luận.

Do \(\sin \alpha  = \dfrac{{\sqrt 6 }}{3} \Rightarrow {\sin ^2}\alpha  = \dfrac{2}{3}\) \( \Rightarrow {\cos ^2}\alpha  = 1 - {\sin ^2}\alpha \) \( = 1 - \dfrac{2}{3} = \dfrac{1}{3}\)

Tử số của P lớn hơn hoặc bằng 2.

Mẫu số là sin² a. cos² a = 2/3. 1/3 = 2/9 < 1/4, nên P ≤ 8.

Do đó các phương án A, B, D bị loại. Đáp án là C.

Cách 2. Tính trực tiếp.

sina = √6/3 ⇒ sin² a = 2/3 ⇒ cos² a = 1/3.

Vậy tan² a = 2, cot² a = 1/2.

Do đó P = 45/4. Đáp án là C.

Đáp án: C

Loigiaihay.com