Toán lớp 11

Bài 5. Phép quay

Câu hỏi 1 trang 16 SGK Hình học 11

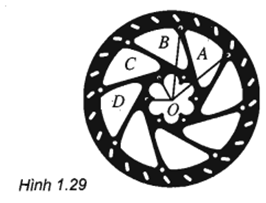
Giải câu hỏi 1 trang 16 SGK Hình học 11. Trong hình 1.29 tìm một góc quay thích hợp để phép quay tâm O....

Đề bài

Trong hình 1.29 tìm một góc quay thích hợp để phép quay tâm O.

- Biến điểm A thành điểm B;

- Biến điểm C thành điểm D.

Video hướng dẫn giải

Lời giải chi tiết

Dễ thấy A, B là hai đỉnh kề nhau của hình bát giác đều nội tiếp đường tròn lớn.

Khi đó \(\left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = \dfrac{{{{360}^0}}}{8} = {45^0}\).

Mà \(OA = OB\) nên phép quay tâm O góc quay \({45^0}\) biến A thành B.

C, D là hai đỉnh kề nhau của hình lục giác đều nội tiếp đường tròn nhỏ.

Khi đó \(\left( {\overrightarrow {OC} ,\overrightarrow {OD} } \right) = \dfrac{{{{360}^0}}}{6} = {60^0}\).

Mà \(OC = OD\) nên phép quay tâm O góc quay \({60^0}\) biến C thành D.

Loigiaihay.com

Bình luận

Bình chọn:

4 trên 5 phiếu

Các bài liên quan: - Bài 5. Phép quay

Báo lỗi - Góp ý

>>Học trực tuyến Lớp 11 trên Tuyensinh247.com, mọi lúc, mọi nơi tất cả các môn. Các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu

Các bài khác cùng chuyên mục