Giải SBT toán hình học và giải tích 12 nâng cao Bài 2. Phương trình mặt phẳng

Bài 49 trang 126 Sách bài tập Hình học lớp 12 Nâng cao


Cho hình hộp chữ nhật ABCD.A’B’C’D’

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A(0;0;0), B(a;0;0), D(0;a;0), A’(0;0;b) với a, b là những số dương và M là trung điểm của CC’.

LG a

Tính thể tích của tứ diện BDA’M.

Lời giải chi tiết:

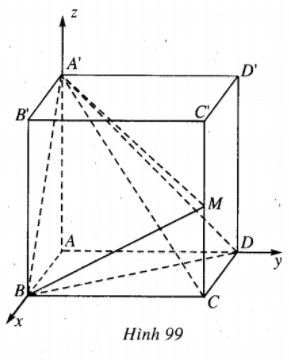
Từ giả thiết ta có C=(a;a;0).

\(C' = (a;a;b) \Rightarrow M = \left( {a;a;{b \over 2}} \right)\)

Ta có \(\overrightarrow {BD}  = \left( { - a;a;0} \right);\)

\(\overrightarrow {BM}  = \left( {0;a;{b \over 2}} \right);\,\,\overrightarrow {BA'}  = \left( { - a;0;b} \right)\)

\( \Rightarrow \left( {\left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right]} \right) = \left( {{{ab} \over 2};{{ab} \over 2}; - {a^2}} \right)\)

Vậy \({V_{BDA'M}} = {1 \over 6}\left| {\left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right].\overrightarrow {BA'} } \right| = {{{a^2}b} \over 4}.\)

LG b

Tìm tỉ số \({a \over b}\) để mp(A’BD) vuông góc với mp(MBD).

Lời giải chi tiết:

Mặt phẳng (A’BD) có vec tơ pháp tuyến

\(\overrightarrow {{n_1}}  = \left[ {\overrightarrow {BD} ,\overrightarrow {BA'} } \right] = (ab;ab;{a^2}).\)

Mặt phẳng (MBD) có vectơ pháp tuyến

\(\overrightarrow {{n_2}}  = \left[ {\overrightarrow {BD} ,\overrightarrow {BM} } \right] = ({{ab} \over 2};{{ab} \over 2}; - {a^2}).\)

Vì vậy

\(\eqalign{  & \left( {MBD} \right) \bot (A'BD) \Leftrightarrow \overrightarrow {{n_1}} .\overrightarrow {{n_2}}  = 0  \cr  &  \Leftrightarrow {{{a^2}{b^2}} \over 2} + {{{a^2}{b^2}} \over 2} - {a^4} = 0  \cr  &  \Leftrightarrow {a^2}{b^2} = {a^4} \Leftrightarrow {a^2} = {b^2} \Leftrightarrow a = b \Leftrightarrow {a \over b} = 1.  \cr  &  \cr} \)

(do \(a > 0,b > 0).\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store